一種適用于小線段的半徑補償 干涉回避算法
2016-12-30 來源:武漢華中數控股份有限公司 作者:吳烜輝 應坤?
【摘要】: 小線段程序在使用半徑補償時出現了刀具干涉報警,首先介紹了法蘭克系統的刀具干涉回避算法,然后給出了通過計算刀補段的交點回避干涉報警的算法,同時對算法的優化進行了討論,最后對算法的效率及有效性進行了測試。
【關鍵詞】: 小線段 半徑補償干涉
引言
在電子信息行業以及飛機、汽車的零配件加工中,由 CAM 等軟件生成的程序,通常由大量的小線段及小圓弧組成。由于效率及成本方面的考慮,通常會在小線段程序中大量使用半徑補償。但是因為 CAM 軟件本身的誤差,或者編程人員的參數選擇不當,有時候會生成有半徑補償干涉的程序,此時數控系統僅給出報警并停止加工的策略是不合適的。數控系統必須能夠自動回避干涉,保證加工的順利進行。
1、法蘭克干涉回避算法
法蘭克系統的干涉回避算法分為兩種情況。一種是連續三段編程軌跡的刀補軌跡發生干涉,如圖 1( 左 ) 所示,V2 和 V5 相互干涉,因此,V2、V5 以及其內側的 V3、V4 被刪除,V1 和V6 被連接起來。另一種情況是相鄰的三段不干涉,但是多段后發生干涉,如圖 1(右)所示,從程序段 1 的終點到程序段 N-1 間建立輔助的“間隙矢量”,對間隙矢量建立刀補軌跡從而回避刀具干涉報警。
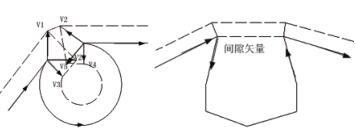
圖1 連續三段的干涉回避 ( 左 ) 和多段的干涉回避 ( 右)
法蘭克系統的干涉回避算法是基于刀具矢量的,具有計算簡單、速度快的優點,但是這種算法對于一些特殊情況無法回避干涉。2、計算刀補段交點的干涉回避算法本文的算法通過直接計算刀補段間的交點來回避刀具干涉。為了判斷刀補段是否有交點,首先需要緩存每段編程軌跡的刀補軌跡信息。為方便討論問題,假設對連續 5 段計算是否有刀具干涉,同時假設每個程序段的刀補段只有一段,則緩存刀補軌跡信息的數據結構如圖 2 所示 :如果兩個刀補段之間有交點,則刪除兩段之間的刀補段。假設計算出了 B1 與 B3 有交點,則刪除B2段,將交點設為B1的終點、B3的起點,再重新計算 B1、B3 的其它程序段信息,調整后的數據結構如圖 3 所示。
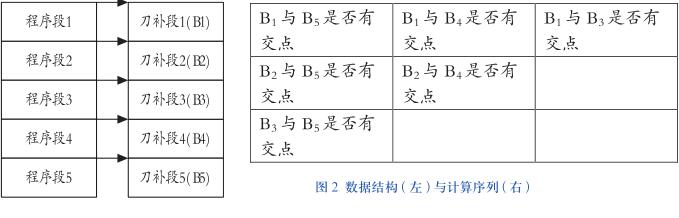
圖 2 數據結構 ( 左 ) 與計算序列 ( 右)
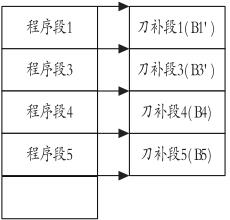
圖 3 有交點后調整緩沖區
3、算法優化
判斷刀補段之間是否有交點分為三種情況 :1)直線段與直線段是否有交點。2)直線段與圓弧段是否有交點。3)圓弧段與圓弧段是否有交點。
首先需要根據直線 / 圓的方程求出交點,然后再判斷交點是否確實落在兩個刀補段上。可見,這種算法的計算量比較大。為了提高算法的效率,首先引入矩形包絡法,就是根據段的起點、終點數據得出包含程序段的最大矩形。如果兩個刀補段的包絡矩形不相交,則兩個刀補段必然沒有交點,如圖 4 所示,因為直線段AB 與圓弧段 CD的包絡矩形不相交,所以AB 段與 CD 段沒有交點。如果兩個刀補段的包絡矩形相交,則兩個刀補段就有可能相交,此時再根據兩個刀補段的直線 / 圓方程計算交點。如果兩個刀補段的方程有解,下一步,就需要判斷這個交點是否同時在兩個刀補段上。對于交點是否在直線段上,只需要簡單的大小比較就能夠判斷出來。對于交點是否在圓弧段上,為了減少計算量,嘗試將圓弧分成四個象限內的單調圓弧段,于是也可以通過簡單的大小比較判斷出交點是否在圓弧段上了。
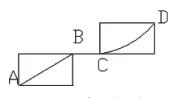
圖 4 矩形包絡法示例
4、算法驗證測試
在華中 8 型數控系統中運行測試程序,第一個測試是運行一個來自深圳某知名加工企業的手機外殼加工程序,為了簡化測試,僅運行發生干涉報警的程序段,測試程序如下 :
%1234
G54 G0 X0 Y0
G41 D01 G01 X-33.458 Y-67.263 ;
N1 X-33.508 Y-67.296;A---->B
N2 X-33.504 Y-67.312;B---->C
G03 X-33.007 Y-68.341 I5.962 J2.244
G40 G01 X-32.567 Y-67.368
M30
1 號刀的刀具半徑為 0.03mm,運行程序的結果如圖 5 所示,虛線表示 G 代碼的編程軌跡,實線部分是 G 代碼的刀補后軌跡,從圖 5(左)可以看到刀補軌跡 A’ B’ 與 C’ D’ 相交于 E’ 點,所以最終回避干涉后的路徑為 A’ ->E’ ->D’。
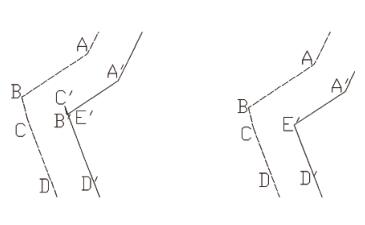
圖 5 發生刀具干涉的路徑 ( 左 ) 與回避干涉后的路徑 ( 右)
第二個測試程序用來測試相鄰三段不干涉,但是間隔多段后發生干涉的情形。測試程序如下 :1 號刀的刀具半徑為 1mm,運行程序的結果如圖 6 所示。
%1234
G54 G0 X0 Y0
G41 D01 G01 X10 Y0
X5 Y-5
X17
X12Y0
G40X20
M30
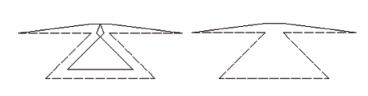
圖 6 發生刀具干涉的路徑 ( 左 ) 與回避干涉后的路徑 ( 右)
第三個測試是算法時間測試,在華中 8 型數控系統上運行一個手機外殼加工程序,同時使用不同的干涉檢測段數得出的結果如表 1 所示。根據表 1 的數據,回避干涉算法時間能夠滿足華中 8 型數控系統 1ms 的插補要求。
4、結語
本文所提出的半徑補償干涉回避算法,雖然計算量較大,但通過算法優化,已經能夠滿足華中 8 型數控系統的要求。而且,這種算法能夠處理文獻 1 中提到的法蘭克系統無法回避干涉的幾種情況。目前,這個算法已經集成在華中 8 型數控系統中,配套的機床在成都某廠飛機零件加工,以及東莞、深圳等地企業電子信息產品零件批量加工中都有應用。
基金項目 :“高檔數控機床與基礎制造裝備”科技重大專項(2013ZX04001-021)

投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com




