T_S模糊模型變結構的機器臂軌跡跟蹤控制①
2016-8-2 來源：江南大學，輕工過程先進控制教育部重點實驗 作者：王憲 盛巍 宋書林 平雪良
摘要：針對不確定性的機械臂軌跡跟蹤問題，結合滑模變結構和T．S模糊模型的優點，給出一種基于T．S模糊模型的變結構軌跡跟蹤的方法。首先采用T．S模型建模，得到機械臂的模糊模型：然后設計出保證機械臂全局漸近穩定的滑模控制器。仿真結果表明，所設計的模糊變結構控制器與普通變結構控制器相比，可使機械臂無論在計算時間、誤差上都具有更大的優勢和更強的魯棒性。
關鍵詞：非線性系統：模糊控制；滑模控制：
1 、引言
機器人軌跡跟蹤控制的主要目的是通過給定各關節的驅動力矩，使得機器人的位置、速度等狀態變量跟蹤給定的理想軌跡【13】。傳統控制方法大都在被控對象數學模型確定、定量化的前提下，卻難以對復雜的、非線性的不確定系統進行有效而又精確的控制。智能控制的出現為解決此類問題提供了新的思路。文獻【l】提出了針對非線性系統的模糊自適應控制理論，為不確定性系統的控制提供一種可行的控制策略：文獻【2．5，11．13】等都對文獻【1】方案進一步改進，取得了多方面進展，但是這些方法都存在一定的問題，如：傳統的滑模控制(SMC)瞄刮因其在滑動模態對系統干擾和攝動具有魯棒性而得到重視，但高頻抖動的問題，以及輸出力矩和跟蹤誤差精度上也有待提高：文獻[11】在文獻【12】的基礎上將滑模控制與飽和函數有機結合，但是在追蹤時間和誤差上都有待商榷。據此分析，為了避免傳統非線性控制器設計方法中迭代計算中近似值以及計算負擔增加的問題，提高伺服控制器對于追蹤誤差和輸出力矩上的控制精度，同時針對所需求的精確性使用適當選取的T．S模糊模型來近似原始非線性模型時，產生一些額外的系統不確定性(unccnain哆)。本文提出一種結合T．S模糊模型與變結構控制的控制器設計方法，這種控制器容易實現且不需要去解J∞obi方程式或不等式，同時運用T．S模糊模型的優點(計算快速)來減輕計算上的負擔；通過仿真并利用兩軸機器臂的模擬來驗證算法的正確性。
2、機器人動力學模型
2．1動力學模型分析
自由度機器人的動力學方程由下式給出：
式中q,q,q,∈Rn為位移、速度和加速度矢量，M(q)∈Rn×n為對稱正定的慣性矩，C(q，q)∈Rn×n為離心和coriolis力矩矩陣，G(q)∈Rn為重力矢量，F(q)∈rn”為摩擦向量，^d為外部未知有界干，f為控制輸入力矩矢量。其中F(q)和d^為可能的不確定項，F(q)是由各種參數誤差、降階處理，以及建模時動態特性所^帶的模型誤差：d^主要指不確定的外部干擾。
機器人動力學方程(2．1)具有如下性質：
性質l：M(q)是對稱正定矩陣，滿足：
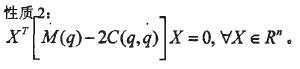
可知當系統的參數精確已知、且結構確定的情況下，控制律能保證閉環系統的全局穩定；但當系統存在結構參數誤差、摩擦及干擾等不確定因素時，控制律就不能保證系統具有良好的動態性和穩定性；同時選擇T-S模型來近似非線性模型、簡化計算時，也會帶不確定性因素。為了消除不確定性的影響。保證系統的漸近收斂，必須設計控制律來彌補T-S模糊模型來近似非線性模型所帶來的不確定性。(其中這里的不確定性主要來自模型誤差即)F(q)。
2．2問題描述
本文以一個二階非線性系統為例，二階非線性系統微分方程如下：
x1=x2
3、模糊變結構控制器的設計
3．1T-S模糊建模
T—S模糊模型是由一組“if-then明”模糊規則來描述非線性系統(2．2)的行為，每一個規則代表一個子系統，整個模糊系統即為各子系統的線性組合。第i條模糊規則對應的模糊狀態方程為：
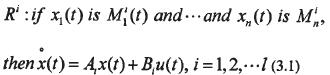
利用(3．2)式可將原始非線性系統改寫成T-S模型：
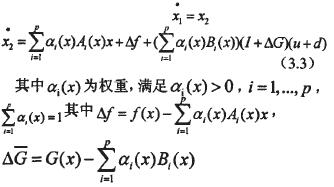
3．2控制器的設計
利用(3．3)式可改寫以下型式：
3．3方法的斂散性
為了讓系統狀態在有限時間內到達順?平面，我們提出以下假設；
也就是系統狀態在有限時間內會到達順滑平面。由以上的討論我們會有以下的結果：
定理3．1：令假設3．1與假設3．2同時成立，則采用控制律(3．7)，(3．8)以及(3．12)時，此系統(2．2)會達到追蹤的性能表現。
4、實驗與仿真
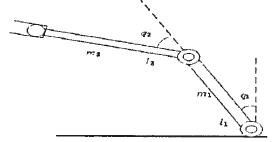
圖4．1兩軸機械手臂示意圖
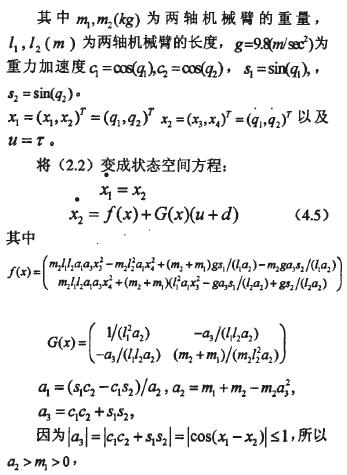
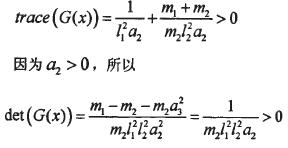
操作點的選定規則如下：
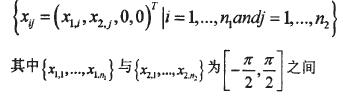
另一方面雖然T_s變結構控制律會比典型非線性變結構控制律需要較多的控制能量，可是在整個過程當中T．s變結構控制律所消耗的總能量有可能會比典型非線性變結構控制律來得少且過程中的總誤差值也比較小。這可能是因為T-s變結構控制律一開始所需的能量較大，一開始能量較大會使得系統狀態能快速地接近目標；而典型非線性變結構控制律一開始所需的能量較小，在過程中隨著狀態越來越靠近目標且越來越靠近順滑平面其所需的能量也一直在變小，所以到達目標的時間會比較長。就總能量說，T-s變結構控制律一開始所需的能量較大，但是隨著狀態快速地到達目標而變小；反觀典型非線性變結構控制律一開始所需的能量雖然比較小，但是接近目標的速度較慢，所以過程中典型非線性變結構控制律所消耗的總能量有可能會比較多。從控制律入能量圖(圖4．3)中可以觀察到會有兩個跳躍現象(Jump)，這是因為系統狀態到達順滑平面的緣故。同時這種情形也可以分別從圖4．2觀察到。在計算時間方面，我們將T-s變結構控制律與典型非線性變結構控制律各計算了106次之后發現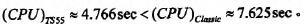
由此可以知道T-s變結構控制律可以節省計算時間。
由此可以知道T-s變結構控制律可以節省計算時間。 表4．1各項性能指標
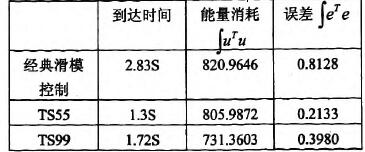
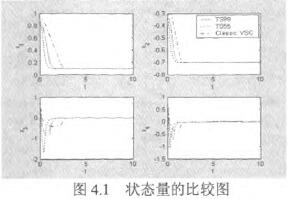
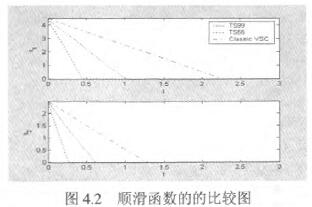
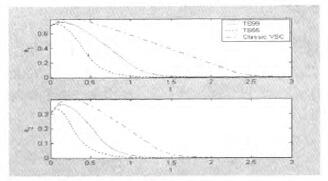
圖4．4誤差的比較圖
5、小結
本文結合了T-s模糊模型與變結構控制理論并且應用在兩軸機器手臂系統上。這種方法可以大量地減輕即時計算的負擔，具有響應快速以及強健的特性。最后，增加模糊法則的數量可以降低控制輸入的大小，也就是將系統操作區間劃分多一點會使得控制輸入變小以至于在實際應用上有控制輸入大小限制時能夠輕易地實現。同時，增加模糊法則地數量并不會造成額外的計算負擔。由模擬的結果顯示，這種結合T．S模糊模型與變結構控制的方法同樣可以完成任務，而且在使用的能量、時間、追蹤誤差上比典型變結構控制方法來得少。
投稿箱：
如果您有機床行業、企業相關新聞稿件發表，或進行資訊合作，歡迎聯系本網編輯部， 郵箱：skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表，或進行資訊合作，歡迎聯系本網編輯部， 郵箱：skjcsc@vip.sina.com
