基于非線性預測的機床主軸溫升特性快速辨識
2017-11-16 來源: 浙江工業職業技術學院 浙江大學機械 作者:馮剛 夏晨暉 孫磊 傅建中
摘要: 提出了一種快速辨識數控機床主軸溫升特性的方法,該方法通過基于支持向量機回歸的非線性預測技術,利用短時間實際采集主軸的溫升數據,預測長達數小時的主軸溫升曲線,并辨識出主軸的穩態溫度、熱平衡時間等溫升特性參數。該方法可大大縮短數控機床主軸熱平衡試驗的時間。試驗研究表明基于支持向量機回歸的非線性預測方法快速辨識的主軸溫升特性與熱平衡試驗結果相吻合,驗證了本文方法的有效性與可行性。
關鍵詞: 機床溫升特性非線性預測支持向量機回歸
引言
數控機床的加工精度是衡量機床工作性能的關鍵指標。隨著機床朝高速高精方向發展,熱誤差所占機床加工總誤差的比重越來越大,達到75% 左右[1 - 2],所以精密數控機床熱態精度設計具有重要的意義。主軸是數控機床的關鍵功能部件,也是機床的最主要發熱源,主軸的熱設計至關重要[3],其溫升特性將很大程度影響機床的加工性能和精度。由于主軸熱結構具有復雜的邊界條件和結合面,其熱設計的理論建模和有限元分析存在較大的誤差[4],必須通過熱平衡試驗以獲取主軸的溫升特性,并校核模型參數。
數控機床開始工作后的熱態特性是一個緩慢變化的過程,相對于機床的靜力學特性、動力學特性的測試研究而言,機床熱平衡試驗周期長,一般依照機床的品種、類型、規格的不同,有很大差別,試驗時間可從數小時到數十小時不等。縮短數控機床熱平衡試驗時間,對提高數控機床熱效應分析效率具有很重要的現實意義。
國際標準化組織在2007 年發布了ISO230-3[5],對數控機床熱效應確定有很好的指導作用,其實質是規范了數控機床熱平衡試驗和分析。但該標準尚未對數控機床熱平衡時間確定做出明確的評定,對如何縮短熱平衡試驗時間也沒有推薦相關的方法。近年來,有文獻報道快速預測機床選點溫升特性的方法,在較大程度上縮短了熱平衡試驗的溫升特性辨識時間,但未考慮復雜熱系統的非線性問題[6 - 7]。非線性預測技術由支持向量機回歸算法實現。基于統計學習理論的支持向量機學習算法[8 - 9],在解決小樣本、貧信息、非線性及高維空間模式識別中表現出許多特有的優勢,因而已被成功應用到模式識別[10 - 13]、時間序列預測[14 - 16]、非線性系統辨識[17 - 20]等方面。由于支持向量機回歸的非線性預測技術在非線性時間預測上的優勢,本文提出基于支持向量機非線性預測算法的機床主軸溫升特性快速辨識方法,僅利用較短時間的溫度測量數據,即可辨識出其溫升特性、穩態溫度及熱平衡時間。
1 、主軸溫升特性快速辨識方法
1. 1 支持向量機回歸非線性預測
非線性支持向量回歸( SVR) ,其基本思想是通過非線性映射Φ 將數據x 映射到高維特征空間,并在這個高維特征空間中進行線性回歸,即




由此回歸函數的模型便可建立。
1. 2 基于非線性預測的溫升特性模型建立
根據1. 1 節所述的支持向量回歸方法,模型輸入輸出的選取至關重要。數控機床主軸溫升模型即為數控機床主軸測試點從機床啟動到機床達到穩態溫度的溫升變化曲線。假設T( k) 為某點k 時刻的溫度,選取k 時刻之前n 個歷史時刻的溫度( T( k -1) ,T( k - 2) ,…,T( k - n) ) 作為輸入,建立T( k) =f( T( k - 1) ,T( k - 2) ,…,T( k - n) ) 的函數關系。當建立這一模型后,由歷史時刻的溫度便可預測未來時刻的溫度。
1. 3 基于非線性預測的數控機床主軸溫升特性快速辨識算法
根據支持向量回歸算法,提出了短時間辨識溫升特性的判據,以一點為例,具體算法為:
( 1) 選擇一段采樣時間下的溫度數據,利用小波濾波方法將原始數據平滑化。
( 2) 根據溫升模型的輸入變量,需要確定最優歷史數據個數n,本文從1 逐漸增大到35,也即循環35 次,將采樣濾波后的溫度數據重新構造成滿足溫升模型的形式,將重構的溫度數據輸入輸出作為支持向量回歸的訓練集。
( 3) 每次循環中,將訓練集的X、Y 分別歸一化處理,然后采用網格搜索的方法確定支持向量回歸中的最優參數懲罰因子C 及高斯徑向基核函數的核寬度σ,采用ε-支持向量回歸機,ε 取0. 001,進行支持向量回歸計算,獲得溫升模型,并且預測出此采樣時間下的溫度變化。
( 4) 將預測的溫度與采樣濾波后的溫度進行比較,采用均方根誤差( RMSE) 衡量,即

( 5) 判斷均方根誤差圖中是否存在最小均方根誤差,且在此點處均方根誤差是否有明顯變化,如果最小均方根誤差處變化明顯( 圖1a) ,則選擇此時的n 值,此時的n 值為最優歷史數據個數,建立起溫升模型; 如果最小均方根誤差沒有明顯變化( 圖1b) ,則增大采樣時間,返回步驟( 1)
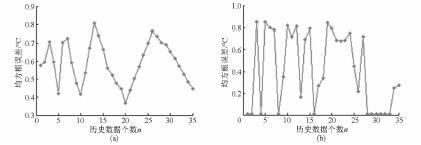
圖1 均方根誤差隨n 的變化曲線
( 6) 根據此采樣時間段內的溫度數據建立溫升模型,即可預測出其后時間的溫度變化情況,達到快速預測的目的。
2 、試驗驗證
為了測量立式加工中心機床主軸的溫度變化情況,需要布置若干測點。圖2 為15 個PT100 型溫度傳感器布置圖,測量環境溫度的傳感器未顯示在圖中,溫度傳感器測量精度0. 1℃,表1 為溫度傳感器布置位置說明。
機床在室溫為18℃環境下,以5 000 r /min 轉速空轉,設置溫度傳感器的采樣間隔為15 s,記錄溫度測量值。本文所提的基于非線性預測的機床主軸溫升特性快速辨識方法,是一種針對一點的溫度測量數據進行處理的方法,所以對每個點來講都是獨立的,對于一個辨識點而言,算法只需要此點的溫度數據,而不需要利用其他點的溫度數據,因而其他測量點的溫度數據對需要辨識的點是沒有影響的。在本文的試驗驗證中,布置了若干測量點,每個測量點都可以分別作為辨識點,來驗證算法的可行性。為說明算法,選擇T5 點來驗證本文提出的算法。T5 點的原始溫度數據如圖3 所示。

圖2 傳感器測點布置圖
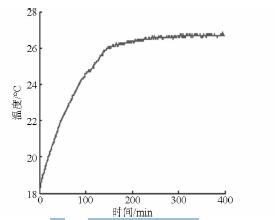
圖3 原始溫度測量數據
將原始測量數據經小波濾波后,其溫度數據如圖4 所示。
表1 溫度傳感器布置位置

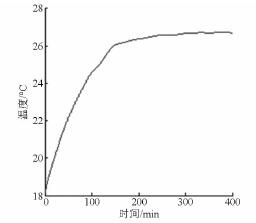
圖4 濾波后的測量數據
基于支持向量回歸的數控機床主軸溫升特性快速辨識算法,得到48 min 內采樣時間下均方根誤差隨n 變化的曲線,如圖5 所示。測量溫度與預測溫度在48 min 內的最小均方根誤差為0. 365 6℃,溫升模型輸入變量的個數為20。基于此溫升模型即可辨識出400 min 的溫升曲線,如圖6 所示。利用48 min 的測量數據,采用基于支持向量回歸的數控
機床溫升特性快速辨識算法,能快速辨識出此點的溫升變化。
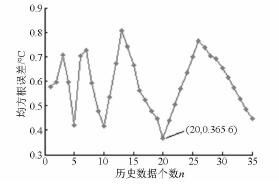
圖5 在48 min 內測量與預測溫度均方根誤差隨n的變化曲線
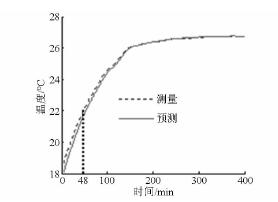
圖6 預測與測量溫升曲線
實測的穩態溫度為26. 7℃,熱平衡時間為126. 25 min( 熱平衡時間定義為到達最大溫升的95%處的時刻) ,預測的穩態溫度為26. 739 2℃,熱平衡時間為130. 5 min。圖7 為測量與預測溫度的誤差圖,從圖中可以看出誤差很小,證明了此預測算法的合理性。
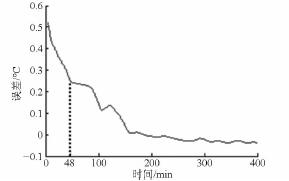
圖7 測量與預測溫度誤差
利用48 min 內的測量數據辨識出溫升模型,當把預測溫度同400 min 的測量溫度進行比較時,得到測量溫度與預測溫度在400 min 內的均方根誤差隨n 的變化曲線,如圖8 所示。從圖中可以看出當模型輸入變量的個數為20 時,出現最小均方根誤差0. 184 8℃。與圖5 比較可以看出,無論是48 min 內還是400 min 內的均方根誤差,在溫升模型輸入個數n 為20 時均出現最小值,且均方根誤差在48 min內或是在400 min 內隨n 變化具有相似性,所以當找到最佳辨識時間48 min 時,辨識的溫升模型即可符合實際溫度變化。
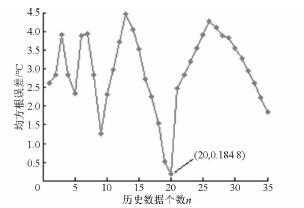
圖8 在400 min 內測量與預測溫度均方根誤差隨
當采樣時間增大到108. 25 min 時,按照上述基于支持向量回歸的數控機床溫升特性快速辨識算法,同樣可以得到在108. 25 min 內測量與預測溫度均方根誤差隨n 的變化曲線,如圖9 所示。從圖9 可以看出有4 個均方根誤差極小值點,選點1 來建立溫升模型。測量溫度與預測溫度在108. 25 min內的最小均方根誤差為0. 194 6℃,溫升模型輸入變量的個數為3。此時預測溫度變化情況如圖10 所示。實測的穩態溫度為26. 7℃,熱平衡時間為126. 25 min,預測的穩態溫度為26. 976 8℃,熱平衡時間為126. 75 min。圖11 為此溫升模型下測量與預測溫度的誤差曲線。
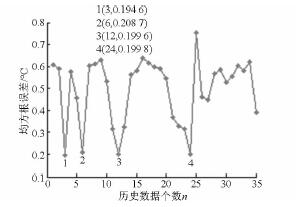
圖9 在108. 25 min 內測量與預測溫度均方根誤差隨
同樣是利用在108. 25 min 內的測量數據,但均方根誤差比較的范圍從108. 25 min 擴大到400 min時,得到測量與預測溫度均方根誤差隨n 的變化曲線,如圖12 所示。對比圖12 與圖9 可以看出,均方根誤差隨n 變化的相似性,且在n 為3、6、12、24 處均有極小值存在。
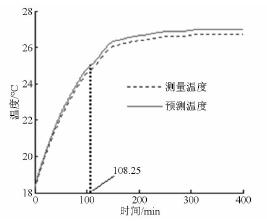
圖10 預測與測量溫升曲線
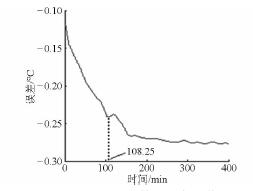
圖11 測量與預測溫度誤差
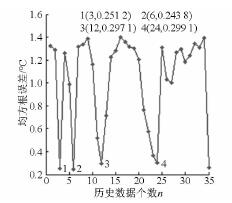
圖12 在400 min 內測量與預測溫度均方根誤差隨n的變化曲線
因此,在采樣時間為108. 25 min 下也可很好地辨識溫升曲線。
本文提出的基于支持向量機的數控機床主軸溫升特性快速辨識算法,可以在若干時間下辨識出溫升曲線,如48 min 和108. 25 min,但是48 min 是其辨識出溫升曲線的最短時間。
同樣地,機床在室溫為18℃ 下,以3 000 r /min轉速空轉,設置溫度傳感器的采樣間隔也為15 s,記錄溫度測量值。依然以T5 為例,T5 點的溫度數據如圖13 所示。
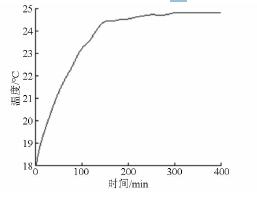
圖13 T5 點濾波后的測量數據
同樣地,基于支持向量回歸的數控機床主軸溫升特性快速辨識算法,得到在40. 5 min 的采樣時間下均方根誤差隨n 的變化曲線,如圖14 所示,測量溫度與預測溫度在40. 5 min 內的最小均方根誤差為0. 300 2℃,溫升模型輸入變量的個數為19。基于此溫升模型即可辨識出400 min 的溫升曲線,如圖15 所示。利用40. 5 min 的測量數據,采用基于支持向量回歸的數控機床溫升特性快速辨識算法,就能快速辨識出此點的溫升變化。
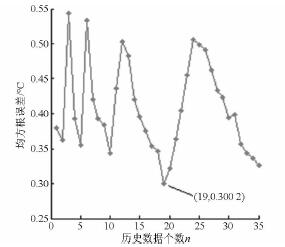
圖14 在40. 5 min 內測量與預測溫度均方根誤差隨n 的變化曲線
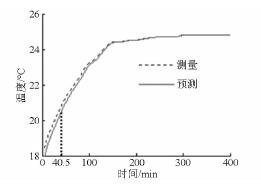
圖15 預測與測量溫升曲線
實測的穩態溫度為24. 8℃,熱平衡時間為150. 25 min,預測的穩態溫度為24. 805 3℃,熱平衡時間為152. 75 min。圖16 為此溫升模型下測量與預測溫度的誤差曲線。
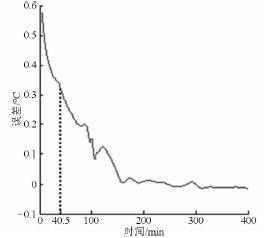
圖16 測量與預測溫度誤差
利用40. 5 min 的測量數據辨識出溫升模型,當把預測溫度同400 min 的測量溫度進行比較時,得到測量溫度與預測溫度在400 min 內的均方根誤差隨n 的變化曲線,如圖17 所示。從圖中可以看出當模型輸入變量的個數為19 時,出現最小均方根誤差0. 154 7℃。與圖14 比較可以看出,無論是40. 5 min內還是400 min 內的均方根誤差,在溫升模型輸入個數n 為19 時均出現最小值,且均方根誤差在40. 5 min 內或是在400 min 內隨n 變化具有相似性,所以當找到最佳辨識時間40. 5 min 時,辨識的溫升模型即可符合實際溫度變化。
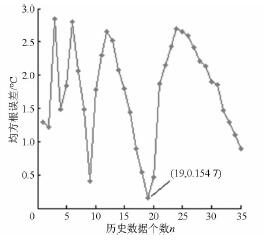
圖17 在400 min 內測量與預測溫度均方根誤差隨n 的變化曲線
改變試驗工況,當機床在18℃ 的室溫下以3 000 r /min 的速率切削試件時,設置溫度傳感器的采樣間隔為15 s,記錄溫度測量值。依然以T5 為例,T5 點的溫度數據如圖18 所示。同樣地,基于支持向量回歸的數控機床主軸溫升特性快速辨識算法,得到在46 min 的采樣時間下均方根誤差隨n 的變化曲線,如圖19 所示,測量溫度與預測溫度在46 min 內的最小均方根誤差為0. 063 1℃,溫升模型輸入變量的個數為11。基于此溫升模型即可辨識出400 min 的溫升曲線,如圖20所示。利用46 min 的測量數據,采用基于支持向量回歸的數控機床溫升特性快速辨識算法,就能快速辨識出此點的溫升變化。
實測穩態溫度為27. 4℃,熱平衡時間為170 min,預測穩態溫度為27. 206 9℃,熱平衡時間為169 min。圖21 為此溫升模型下測量與預測溫度的誤差曲線。
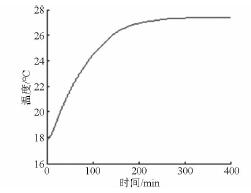
圖18 T5 點濾波后的測量數據
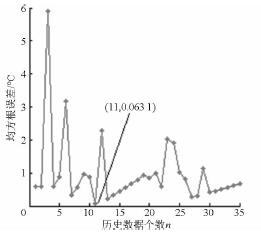
圖19 在46 min 內測量與預測溫度均方根誤差隨n 的變化曲線
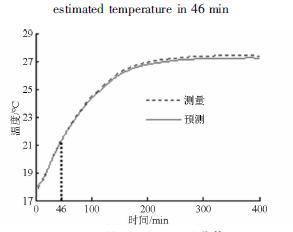
圖20 預測與測量溫升曲線
利用46 min 的測量數據辨識出溫升模型,當把預測溫度同400 min 的測量溫度進行比較時,得到測量溫度與預測溫度在400 min 內的均方根誤差隨n 的變化曲線,如圖22 所示。從圖中可以看出當模型輸入變量的個數為11 時,出現最小均方根誤差0. 147℃。與圖19 比較可以看出,無論是46 min 內還是400 min 內的均方根誤差,在溫升模型輸入個數n 為11 時均出現最小值,且均方根誤差在46 min內或是在400 min 內隨n 變化具有相似性,所以當找到最佳辨識時間46 min 時,辨識的溫升模型即可符合實際溫度變化。
本文提出的基于支持向量回歸的數控機床溫升特性快速辨識算法分別在3 種不同工況下進行了試驗驗證,即主軸在5 000 r /min 轉速下空轉,主軸在3 000 r /min 轉速下空轉及主軸在3 000 r /min 轉速下切削。算法均能在不同轉速條件不同切削條件下實現對主軸選點的溫升特性快速辨識。
主軸系統熱態特性與其動態特性之間存在耦合交互關系,熱變形將使主軸的固有頻率及諧響應發生變化,同樣地,主軸的振動也會影響到熱態特性,但最終都會對機床加工精度產生影響。
3 、結論
( 1) 基于支持向量機回歸的非線性預測方法,可以利用短時間實際采集主軸的溫升數據,預測長達數小時的主軸溫升曲線。進行了試驗,在不同轉速條件及不同切削條件下驗證了該方法的有效性。
( 2) 通過快速辨識主軸的穩態溫度、熱平衡時間等溫升特性參數,可大大縮短數控機床主軸熱平衡試驗的時間。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com





