曲面綜合法弧齒錐齒輪加工參數計算
2016-9-13 來源:河南科技大學機電工程學院 作者:魏冰陽 鄧效忠 仝昂鑫 楊建軍
摘要:針對現有弧齒錐齒輪加工參數計算方法,接觸點綜合紛繁復雜的問題,提出ease.off曲面綜合法。從微分幾何學出發,給出二階密切曲面的定義及其構造方法;在二階精度范圍內,密切曲面與原有曲面具有相同的微分幾何屬性,從而可以替代原有的曲面分析。通過弧齒錐齒輪加工的產成模型,構造大小輪共軛齒面的ease.off差齒面,利用ease.off差齒面的密切曲面完整地拓撲齒面接觸區;利用齒面接觸區的可控參數綜合確定小輪齒面的接觸參數,進而通過數值優化方法求解小輪的加工參數。籍助ease-off密切曲面進行了嚙合仿真,完整呈現了齒面接觸區大小形狀、接觸路徑方向、拋物線失切量等輪齒嚙合信息。所提出的方法適宜于數值方法,基于齒面接觸區的完整性,實現了齒面嚙合性能較好控制。
關鍵詞:二次曲面;輪齒接觸分析:弧齒錐齒輪;差齒面
0前言
弧齒錐齒輪在機械動力傳輸領域具有廣泛的應用,其嚙合理論和制造技術一直是各國專家學者研究的熱點。20世紀90年代起,隨著計算機數值計算方法的應用,弧齒錐齒輪嚙合性能預控理論和設計技術得到快速的發展。LITIVIN等[1-3]發展了“局部綜合”法,預置在參考點二階接觸參數,以期對輪齒傳動誤差和齒面印痕進行控制。吳訓成等[4-6]發展了“主動設計”,通過預置傳動規律,接觸線方向修形,達到對齒面的嚙合性能預控的目的。周凱紅等[7-8]發展了基于預定嚙合特性的點嚙合齒面設
計方法。SIMON等[9-10]發展了弧齒錐齒輪加工參數的優化算法。上述方法均是把曲面嚙合化為點接觸參數,通過接觸點參數的綜合實現對弧齒錐齒輪接觸性能的主動控制。但點接觸參數綜合在對接觸點的矢量、曲率參數計算時,紛繁復雜,多數情況不適合數值方法計算,更不便齒面重構、反求與誤差修正技術的應用。
鑒于上述加工參數計算、嚙合仿真方法的不足之處,本文擬提出一種曲面綜合法,基于齒面接觸過程的完整性,通過ease.off差齒面的密切曲面拓撲接觸區,實現對齒面接觸性能的預控。從微分幾何學出發,給出二階密切曲面的定義及拓撲方法,曲率參數的數值化方法;通過弧齒錐齒輪加工的產成模型,構造ease.off差齒面的密切曲面,通過密切曲面拓撲、接觸參數綜合確定小輪齒面的接觸參數,進而通過數值方法求解小輪的加工參數,最后借助密切曲面完成嚙合仿真。
1、二階密切曲面
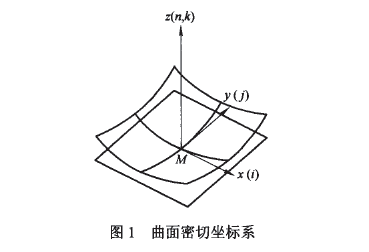
設有一個Σ2類曲面(至少存在2階以上連續微商),在它上面的一點M處取坐標系(Mxyz),如圖1所示,X、Y軸在M點的切平面上,z則在M點的法線刀方向。若曲面Σ2在該坐標系中的方程式為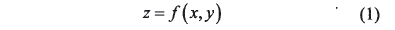
那么,由微分幾何學可以知道【ll】,第1I基本形式為
顯然這是是一個關于(dx,dy)的二次型。
第1I基本形式近似地等于曲面與切平面的有向距離的兩倍,即
由于z軸與M點的法線方向一致,則式(3)表示了z軸的坐標。在小領域內可以用X代替dx,Y代替妙。所以,在M點的鄰域可得到如下近似式
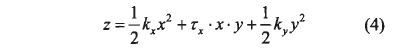
式中 ,
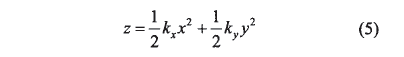
式(4)、(5)表示的曲面Σd和原曲面Σ2在二階項上是一致的,它們有相同的曲率參數 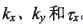 。因此,把Σd為Σ2的二階密切曲面。它們在任意方向上都有相同的法曲率及短程撓率。
。因此,把Σd為Σ2的二階密切曲面。它們在任意方向上都有相同的法曲率及短程撓率。
由于,曲面在正常點的鄰域中總可以有式(1)形式的參數表示,所以總存在一張二次曲面形如式(4),而且當且僅當它們具有相同的曲率參數。因此,這一論述可作為微分幾何的定理給出:
對于Σ2類曲面在正常點的鄰域內,總存在一張與其相切的二次曲面,當且僅當它們具有相同的曲率參數。
由上述分析可以知道,對于Σ2類曲面小鄰域內可以由二階密切曲面代替。本文利用該原理實施弧齒錐齒輪產成曲面的綜合、加工參數的計算及分析。
2、弧齒錐齒輪的產成模型
2.1大輪齒面易產成及其方程
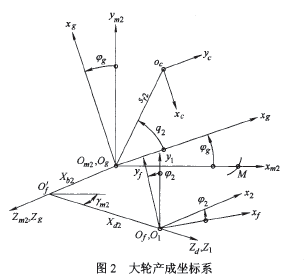
弧齒錐齒輪大輪加工一般采用雙面滾切法,加工參數一般有一致的計算方法。用如圖2所示的坐標系描述大輪齒面的產成。刀盤坐標系 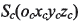 位于瑤臺坐標系
位于瑤臺坐標系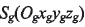 第一象限,繞z軸旋轉,Sg初始位置與機床坐標系
第一象限,繞z軸旋轉,Sg初始位置與機床坐標系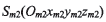 重合,其任意瞬時相對于
重合,其任意瞬時相對于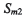 轉角
轉角 ,則大輪相應的產成轉角為
,則大輪相應的產成轉角為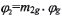 。其余參數
。其余參數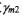 為輪坯安裝角(等于大輪根錐角),
為輪坯安裝角(等于大輪根錐角),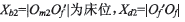 為軸向輪位修正值。根據嚙合方程可推得
為軸向輪位修正值。根據嚙合方程可推得


2.2共軛小輪齒面Σl
利用大輪齒面產成小輪齒面為包絡原理,假設大小輪嚙合的初始角度為庇o、咖o,則任意嚙合位置大小輪之間的轉角的關系為

2.3數值微分求共軛小輪的曲率參數
給定大輪齒面Σ2上參考點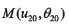 的曲面參數
的曲面參數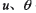 ,并給定微分
,并給定微分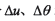 增量,利用上述式(1)~(9)運算,求數值微分
增量,利用上述式(1)~(9)運算,求數值微分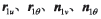 即
即

3 、Ease.off曲面綜合
對共軛小輪齒面Σ 1修形,在計算點M領域內必然能夠構造一個在M點相切的其余鄰域失切的小輪修形齒面,稱為切觸齒面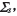 ,相應的主方向、主曲率記作
,相應的主方向、主曲率記作
3.1齒面接觸區拓撲
在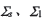 之間沿法線方向構造差曲面稱為ease.off曲面
之間沿法線方向構造差曲面稱為ease.off曲面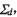 反映了共軛齒面的失切量,該曲面在點M領域可以用形如式(5)的密切曲面代替
反映了共軛齒面的失切量,該曲面在點M領域可以用形如式(5)的密切曲面代替



4、小輪齒面五加工參數的計算
4.1小輪產成模型
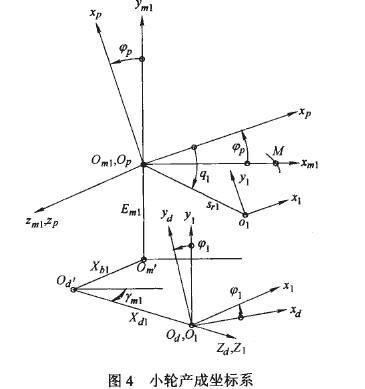
根據小輪產成原理,建立如圖4所示的坐標系來描述小輪的產成過程。刀盤坐標系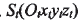
的原點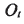 為刀盤中心,
為刀盤中心,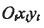 為刀尖平面(與機床平面重合),并與搖臺坐標系
為刀尖平面(與機床平面重合),并與搖臺坐標系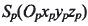
固聯,且各坐標軸對應平行。 在坐標系SP的極坐(
在坐標系SP的極坐(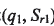 為角向刀位和徑向刀位。Sp初始位置與機床坐標系
為角向刀位和徑向刀位。Sp初始位置與機床坐標系



4.2小輪加工參數計算與仿真
4.2.1 小輪的ant參數的數值求解
利用前述第2.3節的數值微分方法,對式(20)求數值微分,計算小輪的主方向、主曲率,同時將徑矢、法矢統一記作

上述方程是含有小輪加工參數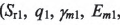
 ,刀盤參數
,刀盤參數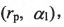 曲紋坐標參數
曲紋坐標參數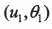
的9個非線性方程組。通過求解該方程組可確定小輪的加工參數。
在求解之前,有些參數是可以首先確定的,輪坯安裝角肋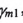 ,刀盤壓力角
,刀盤壓力角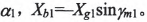
所以實際求解的參數為6個。
式(22)的解的初值和取值范圍是比較容易確定的,所以式(22)適宜用優化的方法求解。本文采用非線性約束優化求解的辦法,利用Matlab優化函數fmincon完成了一個實例計算,結果如表1所示。
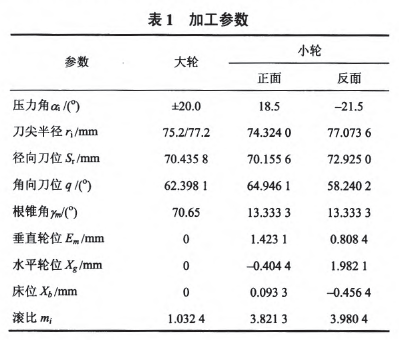
4.2.2 嚙合仿真
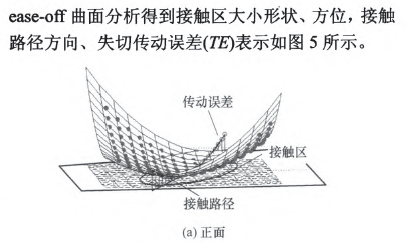
為了驗證表l加工參數計算的準確性,通過構建ease—off差齒面進行接觸仿真,結果如圖5所示ease-off為二次凸曲面,反映齒面接觸呈局部共軛特性,齒面兩端離差在0.04---0.05 mm之間。通過對
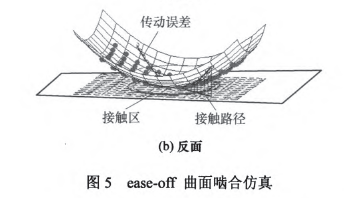
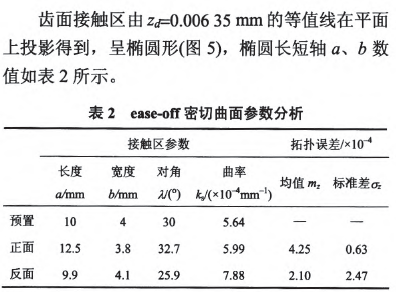

5 、結論
(1)針對現有弧齒錐齒輪N-r參數計算方法,接觸點綜合紛繁復雜,不適宜數值方法計算的不足之處,給出了ease.off曲面綜合法。從微分幾何學出發,給出了二階密切曲面的定義及其拓撲方法;在二階精度范圍內,密切曲面與原有曲面具有相同的微分幾何屬性,從而可以替代原有的曲面分析。
(2)通過弧齒錐齒輪加工的產成模型,構造了ease—off密切曲面,拓撲齒面接觸區;通過曲面綜合確定了小輪齒面的接觸參數,利用數值方法求解出小輪加工參數,借助ease.off密切曲面完成了齒面的嚙合真本文所提出的曲面綜合法適合數值計算,能夠主控齒面接觸區,預置參數能動性較好,嚙合仿真呈現了輪齒接觸的完整信息。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息




