基于結合部的HSK 主軸刀柄系統動態特性分析
2017-2-14 來源:江蘇大學 作者:陳建 王貴成 田良 沈春根 鄭登升
摘要:建立了HSK 主軸刀柄結合部的有限元模型(FEM),利用彈性理論和黏性阻尼理論辨識結合部內各位置的剛度和阻尼參數。提出將HSK 主軸刀柄系統分為HSK 主軸、主軸刀柄結合部和刀柄三部分:HSK 主軸與刀柄簡化為多段Timoshenko 梁,并使用響應耦合法來計算其頻響函數;主軸刀柄結合部簡化為多點彈簧阻尼模型,采用多點響應耦合法來計算其頻響函數;將各個部件的頻響函數進行剛性耦合,進而獲得基于結合部的HSK 主軸刀柄系統頻響函數。分別假定HSK 主軸刀柄結合部為剛性連接、5 點彈性連接和7 點彈性連接,計算其頻響函數,并與實驗結果相比較得到相應的結論。
關鍵詞:HSK 主軸刀柄系統;頻響函數;結合部;動態特性
0.引言
HSK 主軸系統(HSK 主軸刀柄刀具系統)被廣泛應用于高速和高精密加工。加工過程中,影響加工質量和加工效率的主要因素為顫振。獲得準確的穩定性葉瓣圖(切削速度切削厚度關系圖)是避免顫振和保證切削穩定性的必要條件。但無論采用何種方法獲得葉瓣圖,都需先得到機床主軸系統刀尖點的頻率響應函數(FRF)[1]。其中,準確的結合部參數又是精確預測主軸系統刀尖頻率響應函數的前提和保證。本文以HSK 主軸刀柄系統為研究對象,先對HSK 主軸刀柄結合部進行參數辨識,再計算基于結合部的HSK主軸刀柄系統頻響函數。
結合部一般都簡化為彈簧阻尼模型。Ozsahin等[2]采用有限差分法和實驗測量相結合的方式對刀柄刀具結合部進行了參數辨識,再利用單點響應耦合法計算其頻響函數。此方法只能辨識結合部端點的參數,無法辨識結合部內部各個位置的剛度阻尼參數。Namazi 等[3]采用有限元與實驗相結合的方法來辨識結合部參數,并通過有限元法分析其頻響函數,此方法只獲得了結合部內部各個位置的平動剛度和轉動剛度,且其計算量很大,也沒有考慮結合部的阻尼參數。程強等[4]基于子結構耦合法和最小二乘法對BT40 主軸刀柄結合部進行了參數辨識,此方法只獲得了結合部內部各個位置的平動剛度,沒有辨識結合部的轉動剛度和阻尼參數。
基于以上方法的優缺點,提出采用有限元法來辨識HSK 主軸刀柄結合部內部各個位置的剛度和阻尼參數,并使用多點響應耦合法來計算HSK 主軸刀柄系統頻響函數。
1.理論基礎
計算HSK 主軸刀柄系統頻響函數時,可將系統分為HSK 主軸、主軸刀柄結合部和刀柄三個部分,如圖1 所示。HSK 主軸與刀柄都簡化為多段Timoshenko 梁,并使用響應耦合法計算其頻響函數;主軸刀柄結合部簡化為多點彈簧阻尼模型,采用基于Timoshenko 梁理論的多點響應耦合法來計算相應的頻響函數;最終,將各個部件的頻響函數進行剛性耦合,進而獲得基于結合部的HSK 主軸刀柄系統頻響函數。
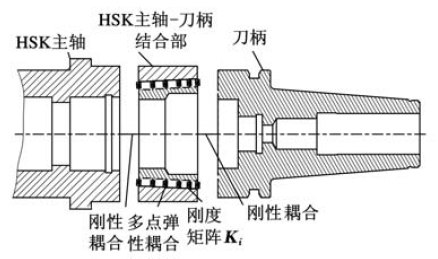
圖1 HSK 主軸刀柄系統的理論模型

1.1 部件頻響函數的理論基礎
在計算HSK 主軸和刀柄的頻響函數時,需將它們都簡化為多段Timoshenko 梁,先分別計算每段梁的頻響函數,再對每段梁進行剛性耦合,進而獲得整個部件的頻響函數。單段梁頻響函數(G 11 )的計算如圖2 所示,梁的兩端點分別表示為1 和2。使用質量集中方程可以建立相應的響應方程,并將與線性和轉動位移有關的力和力矩應用到這些點上。點1 的響應方程可用H 、N 、L 和P 來表示,它們定義如下[6-7]:

圖2 兩自由端均勻Timoshenko 梁


同理,可采用相同的方法對多段梁進行剛性耦合,如圖3b 所示。通過這樣的方式,將不同直徑和長度的梁進行耦合,可計算得到HSK 主軸和刀柄的頻響函數,分別為S 和H 。
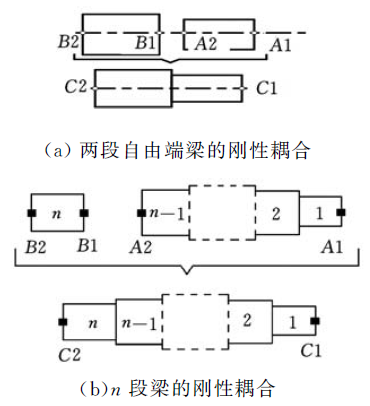
圖3 多段自由端梁的剛性耦合
1 .2 主軸刀柄結合部多點耦合頻響函數的理論
基礎在主軸刀柄結合部取3 個點,分別為兩端點與中心處。結合部的刀柄與刀具都簡化為多段Timoshenko 梁。當n =3 時,總共有6 個坐標點,如圖4 所示,部件(刀具與刀柄)單段的位移/轉角可以表示如下[9-11]:
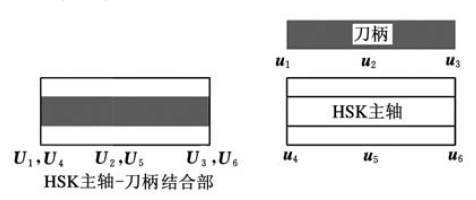
圖4 HSK 主軸刀柄系統及部件
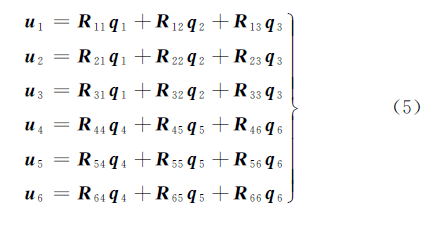


1.3 HSK 主軸刀柄系統頻響函數理論基礎
將計算得到HSK 主軸、HSK 主軸刀柄結合部和刀柄的頻響函數進行剛性耦合,進而得到HSK 主軸刀柄系統的頻響函數:

2. HSK 主軸刀柄結合部的參數辨識
2.1 HSK 主軸刀柄結合部的模型
本文主要使用有限元法來辨識結合部內各個位置的剛度和阻尼參數,為簡化處理,本文假定c yF =cθF 和c yM =cθM [9]。HSK 主軸刀柄結合部規格為A63,主軸和刀柄的材料相同,彈性模量E =500 MPa,密度ρ=7850 kg/m3 ,泊松比μ =0.22。并在結合部處設置接觸面對,目標面為刀柄外錐面,接觸面為主軸內錐面,接觸摩擦因數為0.2,過盈量為10 μm。在刀柄錐面位置施加18 kN的拉緊力,并將主軸末端設置為固定,刀具末端上施加相應的載荷,便可進行熱裝刀柄刀具結合部的參數識別。圖5 所示為HSK 主軸刀柄結合部有限元模型。圖6 為HSK 主軸刀柄結合部關系示意圖。

圖5 HSK 主軸刀柄結合部有限元模型
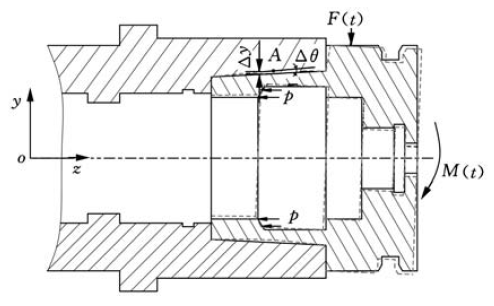
圖6 HSK 主軸刀柄結合部關系示意圖
本文基于彈性理論來辨識結合部的剛度參數。由圖6 所示,拉緊力以均布載荷p 的形式作用在刀柄上,并在刀柄法蘭端面上施加y 方向力F (t ),主軸刀柄結合部上沿z 方向上任意一點A產生的位移為Δy ,A 點的剛度為k yF ,阻尼為c yF 。同樣施加力F (t )時,結合面上沿z 方向上任意一點A 產生的轉動角度為Δθ,A 點的剛度為kθF 。撤去力F (t )后,施加力矩M (t ),A 產生的位移為Δy ,A 點的剛度為k yM ,阻尼為c yM 。同樣地施加力矩M (t ),A 點產生的轉動角度為Δθ,A點的剛度為kθM 。
2.2 HSK 主軸刀柄結合部的剛度辨識
(1)k yF 和kθF 的參數識別。k yF 和kθF 為受力載荷下的剛度,分別在模型上施加1500 N、2000N、2500 N、3000 N 和3500 N 的作用力。設置相應的參數和求解以后,選取結合部上沿z 軸變化的位移Δy ,并繪制每一位置的位移力曲線,斜率即為每一位置的剛度參數k yF ,圖7a 所示為主軸刀柄結合部沿z 軸變化的剛度k yF 。通過計算z軸方向相鄰兩點的位移Δy ,可得沿z 軸各個位置的轉動角度Δθ,繪制每一位置的角度力曲線,其斜率即為剛度kθF ,圖7b 所示為主軸刀柄結合部沿z 軸變化的剛度kθF 。
(2)k yM 和kθM 的參數辨識。k yM 和kθM 為受力矩載荷下的剛度,分別在模型上施加力矩10N.m、12.5 N . m、15 N . m、17.5 N . m、20 N.m。與上述剛度數據處理方法一樣,可得HSK 主軸刀柄結合部沿z 軸變化的剛度k yM 和kθM ,如圖7c 和圖7d 所示。
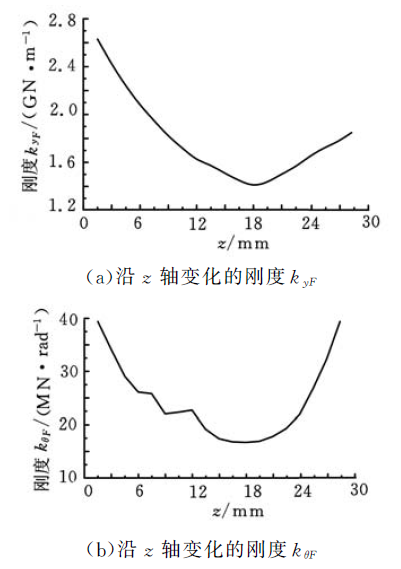
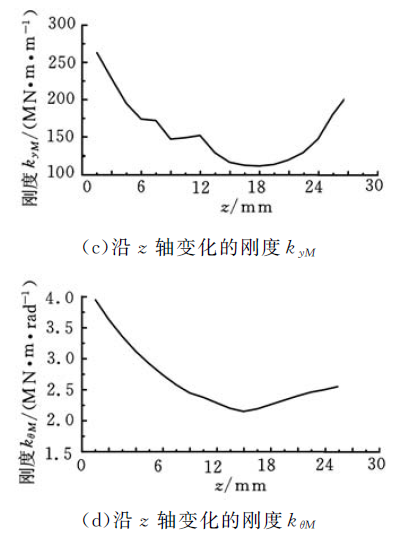
圖7 結合部沿z 軸變化的剛度
HSK 主軸刀柄結合部的4 個剛度變化趨勢都為兩邊剛度大,中間剛度最小。由于HSK 刀柄為中空薄壁結構,雖然主軸/刀柄為過盈配合,但在拉緊力的作用下使得主軸/刀柄中間部分的接觸面積減小,結合部剛度隨之降低;又因為HSK 主軸/刀柄為錐面和端面同時接觸,這使得靠近端面位置的剛度很大。由此可知,拉緊力對HSK 主軸刀柄結合部的剛度影響很大,HSK 主軸/刀柄錐面和端面同時接觸可提高結合部的剛度,此結論與文獻[12-13]所得結論相似。
2.3 HSK 主軸刀柄結合部的阻尼辨識

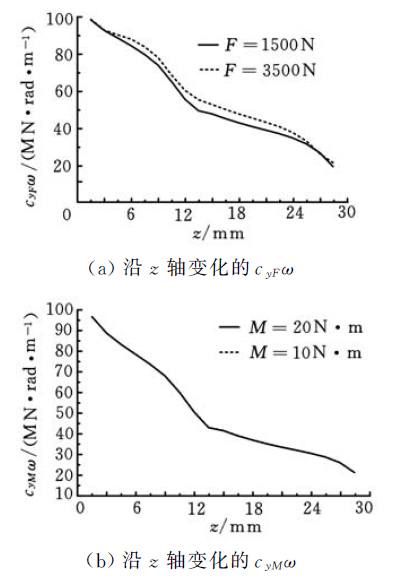
3.實例分析
3.1 HSK 主軸熱裝刀柄系統端點頻響函數
本文以規格為A63 的HSK 主軸[14]和熱裝刀柄[15]為研究對象,如圖9 所示。根據以上的理論基礎,分別將HSK 主軸和熱裝刀柄簡化為多段Timoshenko 梁,具體如表1 和表2 所示。其中,熱裝刀柄的1~10 段和HSK 主軸的43~34段形成錐面結合部。基于有限元法分析獲得了結合部內各個位置的參數,而取多少個點的剛度和阻尼參數對整個系統的頻響函數影響很大。因此,分別考慮HSK 結合部為3 點彈性連接(位置為0、8、16、24 和32)、5 點彈性連接以及剛性連接的情況,并計算HSK 主軸熱裝刀柄端點的頻響函數H SH11 。結合部參數如表3 所示。

圖9 HSK 主軸刀柄系統
表1 HSKA63 熱裝刀柄的分段尺寸mm
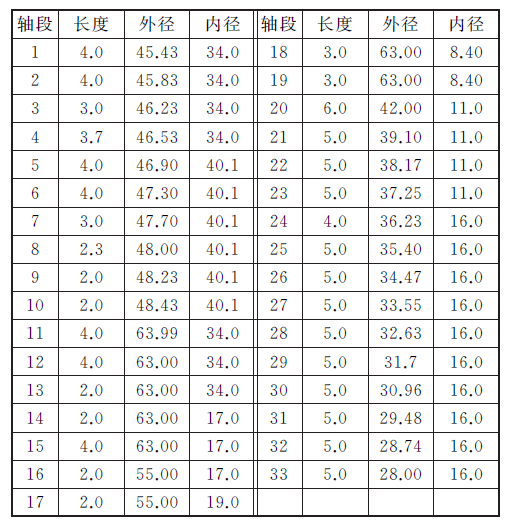
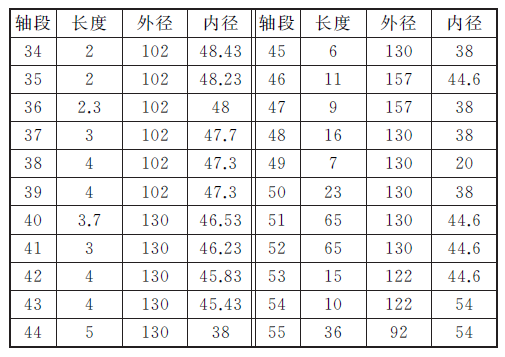
表2 HSK 主軸的分段尺寸mm
3.2 實驗頻響函數
先將HSK 主軸熱裝刀柄系統置于自由狀態;再將Kistler 加速度傳感器安裝在HSK 主軸熱裝刀柄系統端點上;最后,使用力錘敲擊端點處。測量信號通過Cutpro 測試系統進行放大、采集和FFT 轉換,圖10 為實驗頻響函數的測量系統圖。
表3 HSK 主軸刀柄結合部內各個位置的參數
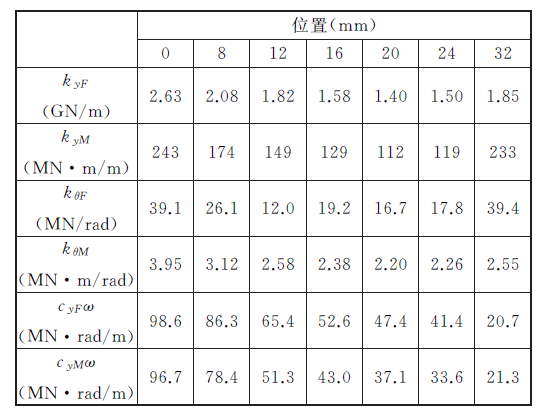
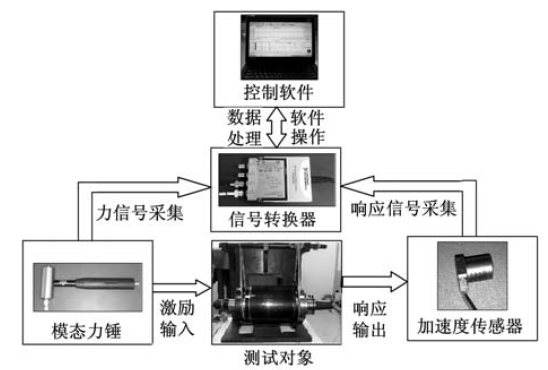
圖10 實驗頻響函數的測量系統圖
根據上述兩種方法獲得HSK 主軸熱裝刀柄端點頻響函數H SH11 ,如圖11 所示。表4 為HSK 主軸熱裝刀柄系統的前5 階模態。
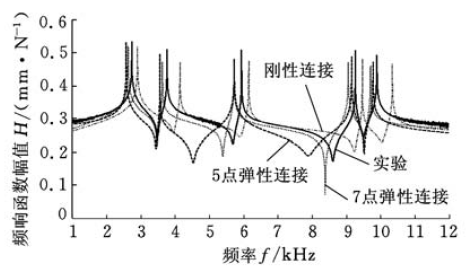
圖1 1 HSK 主軸熱裝刀柄端點頻響函數
表4 HSK 主軸熱裝刀柄系統前5 階模態Hz
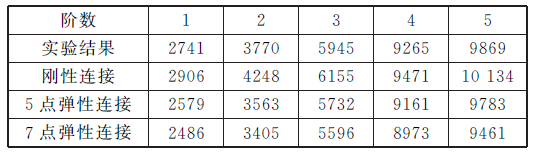
比較HSK 主軸熱裝刀柄系統的各階模態可知,剛性連接的模態比實驗模態更大,并且兩者最大差值達11.3%,因而不能簡單地將HSK 主軸刀柄結合部當作剛性連接來處理。結合部內各點的彈簧阻尼為并聯關系,結合部的整個剛度可等效為各點剛度之和。5 點彈性連接計算的模態與實驗模態最大差值為5.6%,其差值大的原因就是選取點少,整體剛度低。7 點彈性連接計算的模態與實驗模態最大差值為4.2%,與實驗結果很接近。因此,分析HSK 主軸熱裝刀柄系統端點頻響函數時,需考慮HSK 主軸刀柄結合部的影響,并且選用7 點彈性連接來計算系統頻響函數更具有合理性。
4.結論
(1)建立HSK 主軸刀柄結合部有限元模型,使用彈性理論辨識出HSK 主軸刀柄結合部內各個位置的4 個剛度和2 個阻尼參數。
(2)基于多點響應耦合法推導出HSK 主軸熱裝刀柄系統端點頻響函數公式,根據此公式分別計算得到HSK 主軸刀柄結合部為剛性連接、5 點彈性連接和7 點彈性連接的頻響函數。并將其模態值與實驗值相比較可知,分析HSK 主軸刀柄系統頻響函數需要考慮結合部的影響,并且選用7 點彈性連接來計算系統頻響函數更具有合理性。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息




