基于目標規劃的履帶可變形機器人結構參數設計及驗證
2016-9-13 來源:中國科學院沈陽自動化研究所機器人等 作者:朱 巖 王明輝 李 斌 王 聰
摘 要:機器人結構參數直接影響其對環境的適應能力,因此合理的結構參數設計至關重要。為更高效設計能適應障礙已知環境的機器人,該研究提出一種基于目標規劃的機器人結構參數設計方法,以得到能適應該環境的結構參數最優的機器人,并開發樣機進行試驗驗證。首先提出并設計履帶可變形機器人模型,在分析機器人越障機理基礎上,建立機器人能夠跨越的臺階和溝壑障礙與其結構參數間的關系,并在此基礎上建立履帶可變形機器人的結構參數目標規劃模型。利用遺傳算法得到該目標規劃問題的最優結構參數:履帶輪半徑60 mm,擺臂最大長度326 mm,機體長度290 mm,并利用Adams 建立仿真模型驗證了機器人對目標環境的適應性。樣機試驗表明機器人能夠跨越160 mm 高臺階和300 mm寬溝壑,證明了計算得到的結構參數的合理性,及基于目標規劃的機器人結構參數設計方法的可行性。該研究可為機器人的結構參數設計提供參考。
關鍵詞:機器人;遺傳算法;優化;目標規劃;履帶可變形機器人;結構參數
0、引 言
近些年來,機器人已經廣泛應用于救援、檢修、農業和軍事等場合代替人類執行任務。其中,履帶式移動機器人因其較好的環境適應性和較簡單的結構形式,得到了廣泛的研究和應用。目前,已知履帶機器人有Packbot[1]和“靈犀”機器人[2]等履帶不可變形機器人,VCTV-1(variable configuration tracked vehicle-1)機器人[3],VGTV-2 機器人[4],VCTV-3 機器人[5],VGST 機器人[6-8],法國VGTV 機器人[9],NEZA-I 機器人[10]和履帶自張緊式主臂可變構型機器人[11]等履帶可變形機器人。然而多數機器人均針對非結構環境設計,由于非結構環境的復雜性,致使設計得到的機器人較為笨重,應用于核潛艇、室內以及特定農作物種植區等障礙已知的結構環境很不經濟。然而,這樣的環境對于機器人的需求越來越多,尤其是隨著農業對于機器人的需求量日益增大。在農業應用中,農作物行間距以及灌溉溝渠等都是已知障礙,屬于典型的結構環境。機器人機構設計直接影響其對環境的適應性,如何設計合理的機器人本體結構參數成為亟待解決的問題。由于環境障礙的多樣性以及對機器人自身性能的多種要求,例如,在農業應用上,要求機器人能順利通過具有特定行間距的作物并且跨越相應的灌溉溝渠,因此,機器人本體結構參數的設計問題成為多目標優化問題。李楠等[12]使用Pareto 模型處理多目標問題對水陸兩棲可變形機器人的結構參數進行了分析設計,Sergiu 等 [13]使用分量加權方法處理多目標問題對并聯機器人進行了設計分析,劉建等[14]提出了基于多目標粒子群優化算法的礦用救援機器人動力匹配設計方法,Luo Yang[15]采用多目標優化方法設計了輪腿復合機器人Rolling-Wolf。這些設計方法在機器人結構設計研究中均使用性能函數的極值作為設計目標,很難應用于環境障礙已知、對機器人性能提出具體目標要求的環境,因為采用性能極值得到的結構參數值不一定能滿足環境中最大障礙對機器人的要求,即對環境的適應性得不到保障。因此,本文使用目標規劃(goal programming)處理多目標優化問題,將已知環境中障礙最值作為目標賦予性能函數,將性能函數與預期目標間的偏差作為目標函數,以設計最優的機器人結構參數。
本文在分析履帶機器人構型演化機理基礎上,以履帶可變形機器人作為研究對象,將橢圓定理應用于其構型機理設計,進一步在分析機器人越障機理基礎上,建立目標規劃模型,并使用遺傳算法得到可行解,以指導選取合理的機器人結構參數。最后,通過仿真和試驗對機器人結構參數的合理性進行驗證。
1、履帶可變形機器人目標規劃模型
1.1 機器人機構原理設計
1.1.1 概念設計
一般而言,履帶式移動機器人底盤至少需要2 個驅動,以保證機器人可以完成轉向運動。而對于含有擺臂的機器人,其驅動數隨著主動擺臂個數的增加而增加,同時機器人的成本和結構的復雜度也隨之增加,如圖1a所示,是基本的履帶機器人構型演化圖,圖1b 是在假設A 構型越障性能和復雜度均為2 的基礎上對各個構型機器人性能估計值的對比圖。
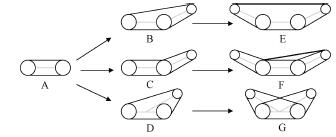
a. A~G 構型推演

b. 構型特性對比
注:對于驅動數,0~10 表示機器人所需的最少驅動數。對于越障性能和結構復雜度,0~10 表示機器人的越障性能和結構復雜度,數值越大,越障性能越強、結構復雜度越大。
圖1 履帶機器人構型推演與構型特性圖
由圖1 可知,構型D 使用3 個驅動和較簡單的結構形式,實現了單臂復用,具有很好的環境適應能力。基于以上考慮,本文對構型D 進行分析研究,設計合理的結構參數,以適應特定的環境。
1.1.2 構型原理設計
對于履帶可變形機器人構型D,設計中要解決的重要問題是如何保證履帶張緊的同時履帶長度不發生變化。如圖2a 所示,可知履帶長度為
式中Lbelt 為履帶的總長度,mm;Lc 為驅動輪O1 和被動輪O2 中心間距,mm;O1P L 為驅動輪中心O1 點到行星輪中心P 的距離,mm;O2P L 為被動輪中心O2 點到行星輪中心P 的距離,mm;ri(i=1,2,3)分別為驅動輪O1,被動輪O2 和行星輪P 的半徑,mm;θi(i=1,2,3)分別為履帶在驅動輪O1,被動輪O2 和行星輪P 上的包角,rad。
假設O1、O2 分別位于橢圓的2 個焦點位置,La 為擺臂最大長度,mm;Lb 為擺臂最小長度,mm;γ 為擺臂OP 與O1O2 連線間的銳角,rad。根據橢圓定義,如果保證擺臂實時長度L 在其旋轉過程中滿足
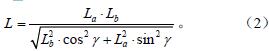
則LO1P + LO2P = 2La 為常數。
由于O1、O2 和P 始終構成三角形,因此,履帶在帶輪上的包角之和始終為2π。假設3 個帶輪半徑相等且均為r,則履帶長度僅與機器人的幾何參數有關,為
采用圖2b 所示彈簧和凸輪機構來實現擺臂按照式
(2)變化且履帶能連續張緊。
注:La 為擺臂最大長度,mm;Lb 為擺臂最小長度,mm;Lc 為驅動輪和被動輪中心間距,mm;γ 為擺臂OP 與O1O2 連線間的銳角,rad;ri(i=1,2,3)分別為驅動輪O1、被動輪O2 和行星輪P 的半徑,mm;θi(i=1,2,3) 分別為履帶在驅動輪輪O1,被動輪O2 和行星輪P 上的包角,rad。
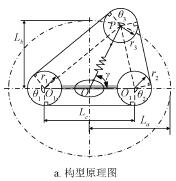
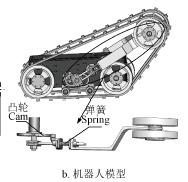
圖2 機器人構型原理及模型
1.2 越障機理分析
為合理規劃機器人結構參數,提高機器人對目標環境的適應能力,需要構建機器人結構參數與能夠跨越的障礙間的關系。本文分析機器人在工作環境中普遍存在的臺階和溝壑2 種不同類型障礙。
1.2.1 攀爬臺階
對于不同大小的臺階,機器人將采取不同策略跨越,當障礙小于驅動輪半徑時,類似輪式機器人,機器人只需前進,無需擺臂的額外輔助即可完成障礙的跨越。當臺階比驅動輪半徑稍大時,可以通過擺臂前擺的方式撐起機體跨越障礙。而機器人能夠跨越的最大障礙是當擺臂后擺撐起機體時,如圖3 所示。
對于較大臺階的跨越,共分為3 個過程:
1)擺臂前擺,支撐起機體,直至機體處履帶與臺階接觸,如圖3a~圖3c 所示;
2)擺臂后擺支撐起機體,同時驅動輪驅動機器人前行,直至機器人重心越過臺階邊界線,如圖3d~3e 所示;
3)擺臂逐漸恢復到越障前的狀態,如圖3f 所示。
機器人越障的關鍵狀態如圖3e,此時機器人重心達到臺階邊界線。假設履帶不彎曲,x 軸平行于與障礙接觸處的履帶,則在機器人剛脫離與地面接觸時應不打滑,滿足
式中Ff 為臺階對機器人的摩擦力,N;FN 為臺階對機器人的支撐力,N;f 為臺階和履帶間的摩擦系數。
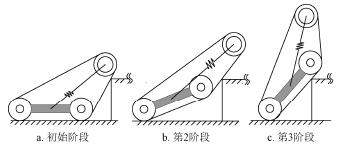
注:X 和Y 分別為直角坐標系的2 個方向,原點位于行星輪中心P 點,X 方向沿P 點指向O2 點,Y 垂直于X;L 為擺臂實時長度,mm;l1 為機體質心G1 到機體幾何中心O 的距離,mm;l2 為擺臂質心G2 到原點P 的距離,mm;β 為x 軸與水平面夾角,rad;H 為臺階高度,mm;Ff 為臺階對機器人的摩擦力,N;FN 為臺階對機器人的支撐力,N。
圖3 機器人攀爬臺階過程
此時臺階高度與機器人質心滿足
式中H 為臺階高度,mm;xG 和yG 分別為機器人重心X軸和Y 軸的坐標值,mm;β 為x 軸與水平面夾角,rad;r 為機器人驅動輪半徑,mm。
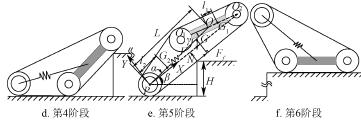
設機器人機體質量為m1,kg;擺臂質量為m2,kg;擺臂與x 軸夾角為α,rad。如圖3e 所示,機器人質心坐標為
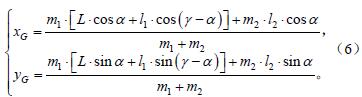
由圖3e 中△OO2P,根據正弦定理可知
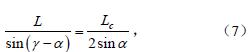
式中α 為擺臂與x 軸夾角,rad。
由式(7)知,γ 確定后,α 也確定。再結合式(6)知,質心位置僅與擺臂實時長度L 和轉角γ 有關。又H對質心的偏導數滿足
因此機器人重心xG 坐標值越大,可以跨越的障礙也越高,顯然增加擺臂長度可以增大xG 坐標值。并且隨著yG 坐標增大,機器人能夠跨越的障礙越小,因此應保證yG 足夠小。
又質心對擺臂OP 與O1O2 連線間的銳角γ 的偏導數滿足
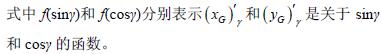
因此擺臂擺動過程中,OP 與O1O2 連線間的銳角γ 越小擺臂越長, 此時能夠跨越的障礙也越大。由于γ ∈[0,90°],可知,當γ=0 時,機器人跨越的障礙最大。
1.2.2 跨越溝壑
對于該擺臂可伸縮式履帶機器人,通過擺臂的前擺和后擺可調節重心位置,可以跨越很大的溝壑障礙。如圖4 所示,機器人跨越較大溝壑過程可以分為2 個階段:
1)擺臂前擺前進直至機器人機體橫跨障礙;
2)擺臂后擺前行直至越過溝壑。
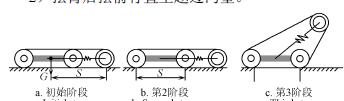
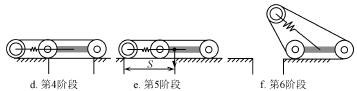
圖4 機器人跨越溝壑過程
由圖4 可知,影響機器人跨越溝壑寬度的為圖4a,圖4b 和圖4e。其中,圖4a 和圖4e 能越過的溝壑寬度由機器人重心到擺臂末端的距離決定,且兩者中較小的距離決定了兩狀態能跨越的溝壑的最大值。又因為機體質心與機體幾何中心存在偏置l1,因此,溝壑長度由擺臂轉向質心偏置方向時決定,為
同理,對式(10)求α 的偏導可知
式中f(sinγ)表示(xGS )α′ 是關于sinγ 的函數。
因此,α 值越小機器人在圖4a 和圖4e 階段跨越的溝壑越寬,又由式(7)可知γ 與α 正相關,同攀爬臺階類似,可得γ=0 時xGS 有最大值。
對于圖4b,此過程中機器人應能夠橫跨障礙,溝壑寬度應不大于Lc+2r,為安全起見,設計溝壑寬度S 滿足
1.3 目標規劃模型建立
1.3.1 目標規劃模型定義

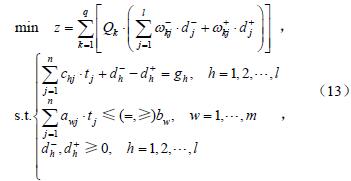
1.3.2 決策變量
機器人跨越障礙的決策變量可以分為2 類,結構參數和越障過程參數。結構參數主要是機器人本身結構影響障礙跨越的幾何尺寸,包括驅動輪O1 和被動輪O2 中心間距Lc,擺臂最大長度La 和驅動輪半徑r 。越障過程參數主要指越障過程中的x 軸與水平面夾角β,則可知決策變量X 為
1.3.3 目標函數及目標約束
假設實際的最高臺階為H0,最寬溝壑為S0,由于攀爬臺階和跨越溝壑均為越障性能,取同一優先級,則標函數為
式中wv 為權重,d1+為超過 H0 的部分,d1−為未達到 H0的部分;d2+為超過S0的部分,d2−為未達到S0的部分。
目標約束為
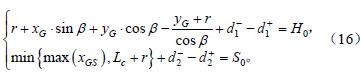
1.3.4 絕對約束
根據機器人越障過程需要滿足的要求以及對變量的估計可以確定模型的絕對約束條件,即必須滿足的條件。
1)越障初始條件約束
機器人若能夠順利跨越障礙,則在準備階段,機器人擺臂必須能夠與臺階邊界線接。
設在跨越障礙前,與障礙接觸時擺臂行星輪中心能達到的最大高度為h0,則根據橢圓定義可知,當行星輪中心與焦點連線垂直于地面時,存在最大值
2)不打滑約束
考慮圖3e 所示臨界狀態處于靜平衡,結合式(4)可得
由于摩擦系數f≤1,因此β 的取值不超過45°,該約束條件可以用于確定邊界約束。
3)邊界約束
邊界約束即為對初始解的估計范圍,給定初始條件可以減少計算時間,提高效率,邊界約束一般形式為

1.4 模型求解
1.4.1 目標規劃模型求解方法
對于目標規劃問題,根據其目標函數以及約束條件是否均為線性,可分為線性規劃問題和非線性目標規劃問題。本文建立的模型包含非線性約束條件,屬于非線性目標規劃問題。對于非線性目標規劃問題,比較傳統的求解方法是線性化逼近算法和模式搜索[16]等。線性化逼近算法對非線性方程的處理比較復雜并且容易產生較大誤差。模式搜索僅能給定一組迭代初值,效率較低。由于遺傳算法多點并行搜索的高效性和準確性[17],采用該種方法求解模型。
1.4.2 遺傳算法的求解過程
遺傳算法是一種基于自然選擇原理和自然遺傳機制的搜索(尋優)算法,它是模擬自然界中的生命進化機制,在人工系統中實現特定目標的優化。其實質是通過群體搜索技術,根據適者生存的原則逐代進化,最終得到最優解或準最優解,已經在工程領域得到廣泛應用。其基本流程如下:
1)編碼及初始化種群。將解變量在邊界約束范圍內映射為遺傳空間的二進制編碼,每個二進制編碼稱為一個個體,每個個體對應所求變量的一組解,并隨機產生N個初始個體作為初始種群。
2)個體的適應度評價。利用適應度函數判斷解(個體)的優劣性,并作為選擇較優解的依據。
3)新種群的產生。通過選擇、交叉和變異產生新的種群個體。
4)終止條件判斷。當進化代數小于設定代數時,返回2)繼續運算;當進化代數達到設定值時,以進化過程中得到的適應度值最大的個體作為最優解,并終止運算。
1.4.3 約束處理
遺傳算法在產生新個體時只能保證產生的個體在所給邊界約束范圍內,對于在邊界約束范圍內,但是不滿足初始條件約束和不打滑約束等非邊界約束的個體沒有得到任何處理。如果直接將其剔除,不但會影響種群數量而且解中的優良基因也將得不到保留,為此筆者引入罰函數,降低此類解的適應度值。由于式(18)可以通過初始條件限制表示,因此只考慮式(17)的罰函數g(X)為
式中M 為較大的常數值。
2、模型驗證
2.1 仿真驗證方法
由于機器人所用履帶屬于柔性體,對于該機器人的仿真屬于剛柔混合仿真,因此建立該機器人仿真平臺的關鍵是建立合適的履帶模型。對于柔性履帶仿真模型有有限元法和剛體分塊法2 種建模方式,考慮到有限元法對計算機硬件的要求比較高,并且計算速度慢,本文采用后者,即建立一系列剛體,各剛體間通過旋轉副連接形成整條履帶。
目前,可對履帶進行分塊仿真的比較流行的軟件是RecurDyn 和Adams。RecurDyn 自帶Track(LM)履帶仿真模塊,但是該模塊適用于大型工程機械,對于像本文提出的機器人使用的履帶,履帶標準中沒有相應型號,對于驅動輪及履帶參數的調試沒有規律可循,筆者最初使用該模塊建立仿真模型,雖然可以進行仿真,但是履帶參數等仍有不合理處,使得仿真時間很長。此外,如果改變機器人結構,仍舊需要對參數進行調整,費時費力。Adams 的帶傳動模塊Belt 可用于履帶的仿真,但是它的履帶塊是通過平面副連接,仿真過程中總是出現履帶塊與塊之間間距過大情況。為此,筆者使用Adams/view 二次開發功能,建立機器人的動力學仿真平臺,使用鉸鏈連接相鄰的履帶塊,并使用STEP 函數驅動機器人運動以驗證其性能。
2.2 試驗驗證方法
通過仿真驗證,初步確定了機器人結構參數的可行性,但是仿真環境與實際環境相比是一種比較理想的環境,得到的機器人結構參數在實際環境的可行性需要進一步的驗證。
如果按照求解得到的機器人結構參數設計的樣機能夠跨越160 mm 高的臺階和300 mm 寬的溝壑,就能保證機器人對核潛艇內環境的適應性,同時也能驗證提出的基于目標規劃的機器人結構參數設計的可行性。
為此,筆者按照計算得到的機器人結構參數,使用SolidWorks 對機器人的機械結構進行了設計,并在中國科學院沈陽自動化研究所機器人學國家重點實驗室完成了加工及裝配,如圖5 所示,機器人主要由行星輪1、擺臂2、驅動輪3、凸輪4、履帶5、被動輪6、驅動輪電機7、蝸輪蝸桿8、擺臂電機9 以及齒輪10 等組成。
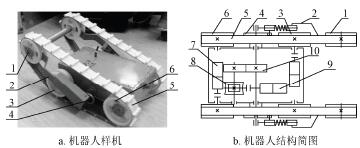
1.行星輪 2.擺臂 3.驅動輪 4.凸輪 5.履帶 6.被動輪 7.驅動輪電機 8.蝸輪蝸桿 9.擺臂電機 10.齒輪
圖5 機器人樣機及結構簡圖
考慮到空間的緊湊性以及可行性,機器人采用電機經減速器減速后直接驅動的方式。由于擺臂擺動過程中需要撐起機體,需要的力矩較大,并且考慮到自鎖性能的需要,在經過減速器后采用蝸輪蝸桿傳動。由于機器人機體長度僅有290 mm,如果蝸輪直接安裝于擺臂軸,擺臂電機的安裝空間僅有機體的一半,很難容納下整個電機,為此經蝸輪蝸桿傳動后增加齒輪傳動將扭矩輸出到擺臂軸,如圖5b 機器人結構簡圖所示。
2.3 結果與分析
2.3.1 機器人機構參數理論計算結果
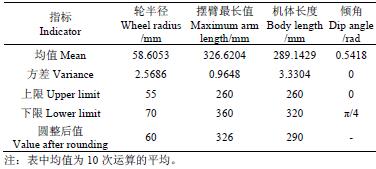
根據對核潛艇實際環境的測量,可以得到環境中最高臺階H0=160 mm,最寬溝壑S0=300 mm。由于所取目標均是越障性能目標,則設定為同一優先等級且權重相等。根據環境中障礙大小以及對機器人的要求,對所求取的參數進行了估計,各設計變量的估計上下限如表1所示。
表1 設計變量上下限及優解
計算過程中,種群數量設置為100,進化代數為100,交叉概率為0.07,變異概率為0.005。應用MATLABR2013a 完成了求解算法程序的編寫,并對程序運行10次,以期獲得最優參數。
由于初始種群的隨機性,以及進化代數的影響,加之計算中保留小數后4 位的精度,多次運行得到的結果會存在微小的波動,為此取10 次計算結果的均值作為結構參數的參考值,并將數值圓整,可得到機器人的結構參數值:履帶輪半徑60 mm,擺臂最大長度326 mm,機體長度 290 mm,如表 1 所示。此時 d1+ = 0.0923 ,d2 0.3706 − = ,可見,跨越溝壑理論上存在稍微不足,但是由于跨越溝壑過程中僅僅考慮了重心到輪心的距離,對于機器人輪心之外的半徑長度可以彌補d2−這一微小偏差。為了驗證結構參數的可行性,采用圓整的尺寸,建立動力學仿真平臺進行驗證。
2.3.2 仿真驗證結果
1)攀爬臺階仿真驗證
根據對核潛艇環境障礙的實測值,設置160 mm 的臺階障礙,并利用Adams 中的STEP 函數對機器人的越障過程進行規劃,其越障過程如圖6 所示。
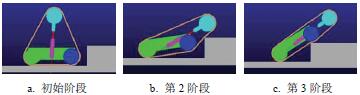
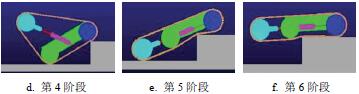
圖6 機器人攀爬臺階仿真
圖6 可知,機器人能順利跨越高度為160 mm 的臺階,從Adams 的后處理模塊Postprocessor 可以得到攀爬臺階過程中驅動輪以及擺臂所需的驅動力變化情況,如圖7所示。越障過程中擺臂需要的驅動力矩最大為21.4653N·m,驅動輪所需驅動力矩最大為5.604 N·m。
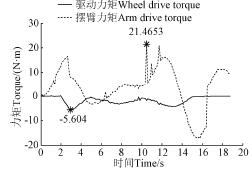
注:-5.604 N·m 是驅動輪所需的最大力矩,21.4653 N·m 是擺臂所需最大力矩。
圖7 機器人攀爬臺階驅動力矩
2)跨越溝壑仿真驗證
同攀爬臺階類似,根據實際溝壑寬度,設置了300 mm寬的溝壑模型,并利用STEP 函數完成了機器人的越障仿真,其跨越溝壑過程如圖8 所示。
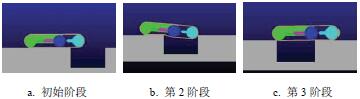
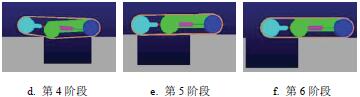
圖8 機器人跨越溝壑仿真
圖8 表明,機器人能順利跨越寬度為300 mm 的臺階,同攀爬臺階類似,可得跨越溝壑過程中驅動輪以及擺臂所需的驅動力如圖9 所示。由圖9 可知,跨越溝壑過程中擺臂所需的最大驅動力矩為20.4987 N·m,驅動輪所需的最大驅動力矩為2.842 N·m。
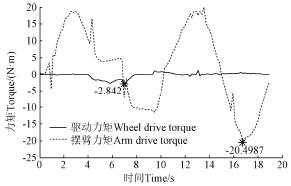
注:-2.842 N·m 是驅動輪所需的最大力矩,-20.4987 N·m 是擺臂所需最大力矩。
圖9 機器人跨越溝壑驅動力矩
綜上可知,所設計的結構參數能夠適應環境中的障礙,可以進行樣機的設計,且通過仿真得到了機器人擺臂以及驅動輪所需的驅動力矩,可以指導機器人設計中電機的選取。同時也初步證明了基于目標規劃的機器人結構參數設計的有效性。
2.3.3 樣機試驗驗證結果
1)攀爬臺階
按照核潛艇內環境障礙,布置了高度為160 mm 的臺階,機器人的越障過程如圖10 所示。首先使機器人前行直至擺臂處履帶與障礙接觸(圖10a);再控制擺臂向有障礙方向擺動支撐起機體(圖10b),同時使機器人緩慢前行,當機體部分履帶與障礙接觸后(圖10c),使機器人停止前行,僅控制擺臂向后擺動直至擺臂撐起機器人(圖10d~圖10e);此時,停止對擺臂的控制,驅動機器人前行,最終機器人能夠順利攀爬臺階(圖10f)。


圖10 機器人攀爬臺階試驗
按照以上步驟進行了多次攀爬臺階試驗,機器人均能順利跨過障礙值。并且將臺階高度增加到170 mm 進行試驗,機器人仍舊順利跨越了障礙,當增加到180 mm 時機器人沒能越過障礙。
可見,實際設計的機器人滿足環境中臺階障礙的要求,并且能攀爬的臺階高度超出預期高度相對也較小,這證實了基于目標規劃的機器人結構參數設計的可行性。對于超出部分可能是由于實際加工以及裝配中的偏差所致,也可能是由于履帶是柔性體,在與障礙接觸過程中,產生微小形變引起的。因為履帶的微小形變會增大機器人與障礙之間的摩擦力并且使得在跨越障礙過程中的關鍵狀態(圖3e)機器人的重心更低更穩定,而在參數計算過程中并沒有考慮履帶變形的影響。
2)跨越溝壑
同攀爬臺階類似,根據環境要求設置了300 mm 寬的溝壑進行試驗驗證,機器人越障過程如圖11 所示。首先驅動擺臂轉動,同時驅動機器人緩慢前行,直到機器人機體橫跨溝壑,再使擺臂后擺直至與地面接觸,然后驅動機器人前行,最終機器人順利跨越了300 mm 寬的溝壑。同樣將溝壑每次增寬10 mm 進行多次試驗過程中發現,當溝壑增大到330 mm 時機器人沒能跨越溝壑。這主要是因為在理論計算中,為了安全起見,取圖4b 中的條件滿足Lc+r 而不是Lc+2r 所致。


圖11 機器人跨越溝壑試驗
通過以上試驗,充分驗證了機器人對環境障礙的適應性,并且超出預期跨越障礙值也較小,也證明了基于目標規劃的機器人結構參數設計方法的有效性。
3、結論與討論
針對差異化障礙環境下的機器人結構參數設計問題,提出了基于目標規劃的機器人結構參數設計方法。通過建立機器人結構參數與環境障礙之間的函數關系,得到機器人越障的性能函數,結合需要跨越的障礙值,建立目標規劃模型,然后利用遺傳算法求解得到最優的結構參數值:履帶輪半徑60 mm,擺臂最大長度326 mm,機體長度290 mm。經試驗驗證,利用得到的參數設計的機器人能夠跨越160 mm 高臺階和300 mm 寬溝壑,并且能跨越的最高臺階和最寬溝壑與期望值相差較小。該方法能夠得到適應該環境的機器人結構參數的盡可能小的值,不但可以減少機器人設計成本,還可以保證機器人在滿足環境要求的前提下盡可能的輕便。此外,該方法也可以用于其他環境障礙要求下的其他類型機器人的結構參數設計。
本文提出基于目標規劃的機器人結構參數設計的最初目的是使得設計的機器人剛好能滿足環境中障礙的要求。但試驗過程中發現,機器人實際能跨越的障礙稍大于預期的障礙,可能的主要原因是,在參數計算時沒有考慮履帶的形變對越障的影響,因此,下一步計劃對履帶形變對機器人越障性能的影響進行研究。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息





