自拍亚洲欧美,7m视频成人精品分类,www.9999av

您現(xiàn)在的位置：機(jī)器人> 技術(shù)前沿>機(jī)器人的運(yùn)動軌跡插值方法研究與分析

機(jī)器人的運(yùn)動軌跡插值方法研究與分析

2016-12-5 來源：陜西理工學(xué)院陜西省工業(yè)自動化重點(diǎn)實(shí)驗(yàn)室作者：趙川張鵬超潘曉磊呂海立

軌跡規(guī)劃對工業(yè)機(jī)器人能夠高效、穩(wěn)定的運(yùn)動有重要的影響。機(jī)器人工作時必須保證運(yùn)行軌跡的平滑。若各關(guān)節(jié)的速度和加速度突變或者不連續(xù)會在機(jī)器人工作過程中，加劇機(jī)構(gòu)的摩擦，機(jī)械臂出現(xiàn)振動現(xiàn)象，增大軌跡跟蹤誤差，降低跟蹤精度，縮短機(jī)器人的使用壽命。為此學(xué)者們提出了多項(xiàng)式插值、B樣條曲線插值等插值方法，從而得到關(guān)節(jié)速度和加速度平穩(wěn)、光滑且連續(xù)的軌跡。

本文通過在MATLAB環(huán)境中仿真研究了三次多項(xiàng)式與五次多項(xiàng)式插值后，各關(guān)節(jié)的關(guān)節(jié)角度位置、速度和加速度的變化軌跡，通過研究分析提出了過路徑點(diǎn)的點(diǎn)到點(diǎn)運(yùn)動間的“353”∽1多項(xiàng)式插值，并且得到了關(guān)節(jié)速度和加速度的平滑連續(xù)的變化軌跡。

1.機(jī)器人運(yùn)動學(xué)模型

本文以NACHI的六自由度MZ07工業(yè)機(jī)器人作為模型研究，確定機(jī)器人的連桿D—H坐標(biāo)參數(shù)，如表1所示，在MATLAB中構(gòu)建機(jī)器人的數(shù)學(xué)模型，如圖1所示。

表1 MZ07機(jī)器人連桿D—H參數(shù)

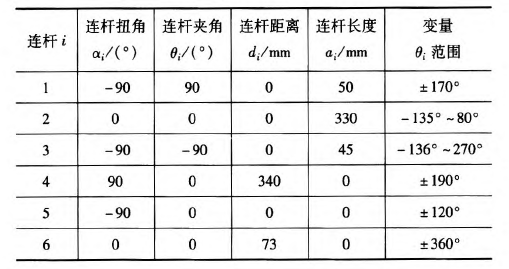
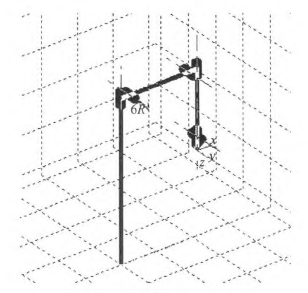
圖1機(jī)器人MATLAB=維模型

2.關(guān)節(jié)空間軌跡插值研究

關(guān)節(jié)空間法是以含有關(guān)節(jié)角度的函數(shù)來描述機(jī)器人的軌跡，在進(jìn)行關(guān)節(jié)空間軌跡規(guī)劃時，需要通過運(yùn)動學(xué)的逆解，將路徑點(diǎn)轉(zhuǎn)換成關(guān)節(jié)矢量角度值，再通過對每個關(guān)節(jié)擬合一個光滑函數(shù)，使從起始點(diǎn)開始，依次通過所有路徑點(diǎn)，最后到達(dá)目標(biāo)點(diǎn)。對于每段路徑，每個關(guān)節(jié)運(yùn)行時間均相同，則保證了所有關(guān)節(jié)同時到達(dá)路徑點(diǎn)和目標(biāo)點(diǎn)，此外，各個關(guān)節(jié)函數(shù)之間是相互獨(dú)立存在的。采用關(guān)節(jié)空間法不需要在直角坐標(biāo)系中描述兩個路徑點(diǎn)之間的路徑形狀，所以計(jì)算簡單、容易，并且關(guān)節(jié)空間不會發(fā)生在直角坐標(biāo)空間中的機(jī)構(gòu)奇異性問題。

2．1過路徑點(diǎn)的三次多項(xiàng)式插值

在單個關(guān)節(jié)運(yùn)動過程中，為了使其能都平穩(wěn)地運(yùn)動，要求關(guān)節(jié)在起始點(diǎn)速度和目標(biāo)點(diǎn)速度均要為0，而且關(guān)節(jié)起始角吼已知，終止點(diǎn)所可由運(yùn)動學(xué)反解求得，則一個三次多項(xiàng)式可由起始點(diǎn)的關(guān)節(jié)角度、速度和終止點(diǎn)的關(guān)節(jié)角度、速度4個約束唯一確定。因此對三次多項(xiàng)式：

由上確定的三次多項(xiàng)式的系數(shù)可以代人式(1)、(2)中，分別可以得到單個關(guān)節(jié)此時刻的的關(guān)節(jié)角度、關(guān)節(jié)速度以及加速度。

但是在現(xiàn)實(shí)應(yīng)用中，要求規(guī)劃出過路徑點(diǎn)的軌跡，然后在經(jīng)過路徑點(diǎn)時的機(jī)器人手臂末端狀態(tài)會有兩種情況：一種情況是機(jī)器人手臂由起始點(diǎn)運(yùn)動到路徑點(diǎn)時停留，即此時的在路徑點(diǎn)處的速度為零，則可以直接使用前面的三次多項(xiàng)式插值算法；另一種情況是機(jī)器人手臂由起始點(diǎn)運(yùn)動到路徑點(diǎn)時不做停留，此時的速度已經(jīng)不再為零，則該點(diǎn)再運(yùn)動到目標(biāo)點(diǎn)或者下一個路徑點(diǎn)時，不能采用前面的三次多項(xiàng)式算法，故上式需要推廣成為具有任意約束速度的三次多項(xiàng)式插值。在過路徑點(diǎn)的軌跡中，可以把所有的路徑點(diǎn)看做是“起始點(diǎn)”或者“目標(biāo)點(diǎn)”，通過求解其逆解，得到各關(guān)節(jié)的關(guān)節(jié)矢量值，然后確定一個三次多項(xiàng)式插值函數(shù)，使各個路徑點(diǎn)平滑地連接起來。只是此時的“起始點(diǎn)”與“目標(biāo)點(diǎn)”處的速度不再為零。在確定此三次多項(xiàng)式的方法與前面所述方法相同，只是改變了速度約束，即：

對于各路徑點(diǎn)處的關(guān)節(jié)速度，我們采用平均值法來確定，規(guī)定各路徑點(diǎn)間的運(yùn)動時間均相等，路徑點(diǎn)速度可根據(jù)兩側(cè)的軌跡的角速度取平均值。如果對于運(yùn)動軌跡的要求更加嚴(yán)格，則需要更高階的多項(xiàng)式對運(yùn)動軌跡進(jìn)行插值。但不是階數(shù)越高越好，高階多項(xiàng)式軌跡會出現(xiàn)“龍格”現(xiàn)象。本文針對五次多項(xiàng)式進(jìn)行研究。五次多項(xiàng)式可由6個約束唯一確定，即在起始點(diǎn)和目標(biāo)點(diǎn)規(guī)定了關(guān)節(jié)位置、速度和加速度，從而來約束整個運(yùn)動軌跡。五次多項(xiàng)式即：

2．3仿真研究

在MATLAB中對MZ07機(jī)器人的運(yùn)動進(jìn)行軌跡規(guī)劃仿真，設(shè)有起始點(diǎn)A(一100，0，一300)、中間點(diǎn)曰(325，225，100)和目標(biāo)點(diǎn)C(235，300，400)。從A點(diǎn)運(yùn)動到B點(diǎn)用時1 s，從B點(diǎn)到c點(diǎn)用時1 S，求得三點(diǎn)的關(guān)節(jié)變量值，如表2所示。

表2軌跡點(diǎn)的關(guān)節(jié)角度

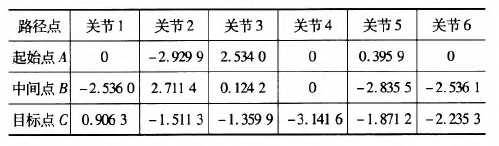
假定該運(yùn)動的起始點(diǎn)與目標(biāo)點(diǎn)的速度與加速度均為零。分別對該三點(diǎn)間的運(yùn)動應(yīng)用三次多項(xiàng)式插值和五次多項(xiàng)式插值，分別得到該過程中關(guān)節(jié)角度、速度和加速度的變化情況，如圖2～7所示，三次多項(xiàng)式與五次多項(xiàng)式插值后的關(guān)節(jié)角度、角速度和角加速度的產(chǎn)生的最大值如表3所示。

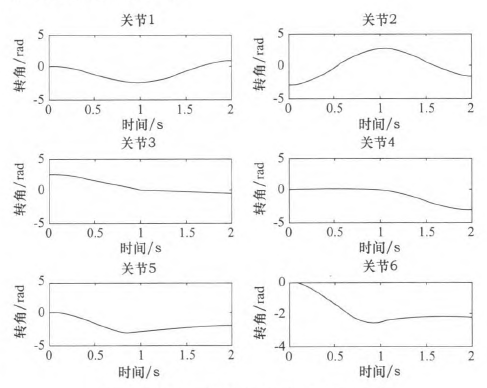
圖2三次多項(xiàng)式規(guī)劃后關(guān)節(jié)i一6角度位置

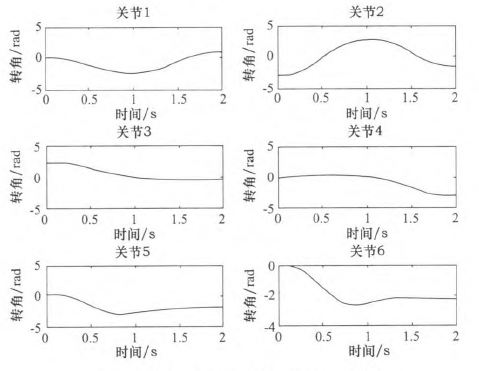
圖3五次多項(xiàng)式規(guī)劃后關(guān)節(jié)卜6角度位置

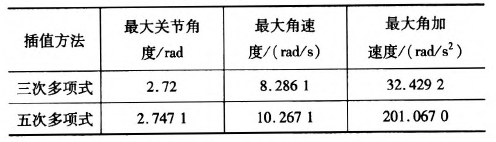
由仿真結(jié)果可知，三次和五次多項(xiàng)式都可以使運(yùn)動軌跡平滑連續(xù)，但是三次多項(xiàng)式插值后，在關(guān)節(jié)加速度上出現(xiàn)突變，現(xiàn)實(shí)中機(jī)器人手臂在運(yùn)動中很可能無法完成此運(yùn)動過程。五次多項(xiàng)式的加速度雖然可以光滑地連續(xù)起來，但是最大角加速度達(dá)到-j'201．067 0rad／s2，使運(yùn)行不夠平穩(wěn)緩和，也有害電動機(jī)的壽命。

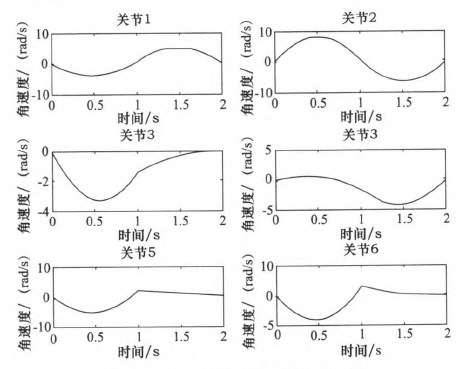
圖4 三次多項(xiàng)式規(guī)劃后關(guān)節(jié)1~6角速度

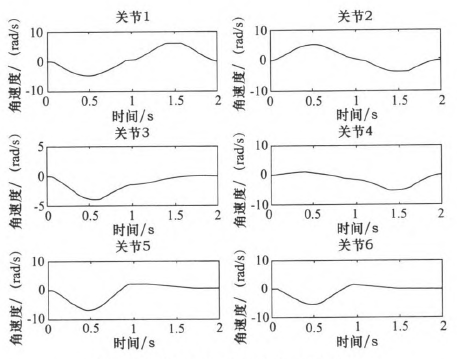
圖5 五次多項(xiàng)式規(guī)劃后關(guān)節(jié)1~6角速度

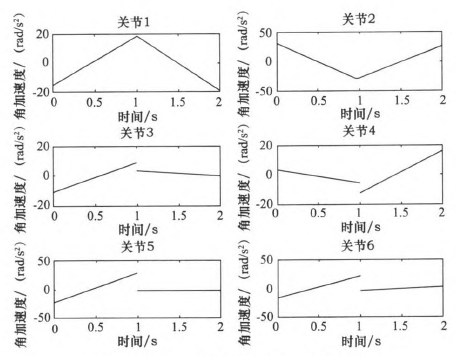
圖6三次多項(xiàng)式規(guī)劃后關(guān)節(jié)1-6角加速度

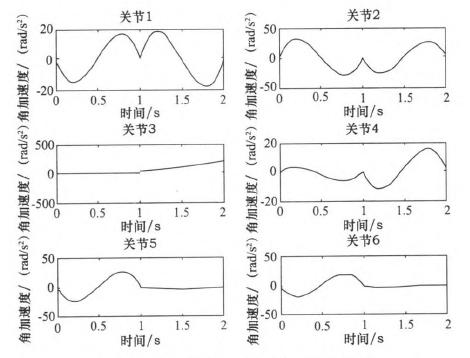
圖7五次多項(xiàng)式規(guī)劃后關(guān)節(jié)1～6角加速度

表3三次多項(xiàng)式與五次多項(xiàng)式最值比較

2．4過路徑點(diǎn)的“353”[gj多項(xiàng)式插值。

在實(shí)際對機(jī)器人運(yùn)動軌跡規(guī)劃時，要求規(guī)劃過路徑點(diǎn)的軌跡，為了得到加速度合適且連續(xù)、平滑的變化軌跡，介于三次多項(xiàng)式和五次多項(xiàng)式的優(yōu)缺點(diǎn)，采用了“353”一1多項(xiàng)式插值，即三次多項(xiàng)式與五次多項(xiàng)式結(jié)合的形式。如圖8所示，該方法將整個軌跡分為3個階段，第一階段為在0一t。時間內(nèi)采用三次多項(xiàng)式插值，第二階段t。一t。時間內(nèi)采用五次多項(xiàng)式插值，第三階段t。一t，時間內(nèi)采用三次多項(xiàng)式插值。本結(jié)構(gòu)方法的要求，在兩個相鄰階段的交點(diǎn)處的關(guān)節(jié)角度、角速度和角加速度要求相等。其中t。、t6可分別取0一t^、t^一f，時刻的中間時刻。

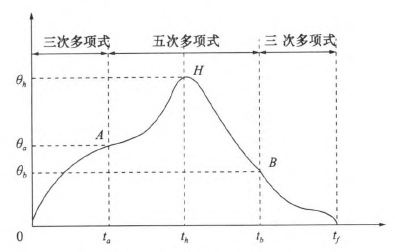
圖8“353”多項(xiàng)式結(jié)構(gòu)

同樣使用2．3節(jié)假定的A、B、c三點(diǎn)。在MATLAB中仿真出“353”多項(xiàng)式結(jié)構(gòu)算法規(guī)劃后的各關(guān)節(jié)的關(guān)節(jié)角度、角速度和角加速度變化情況，如圖9—10所示。規(guī)劃后的關(guān)節(jié)角度、角速度和角加速度的最大值如表4所示。

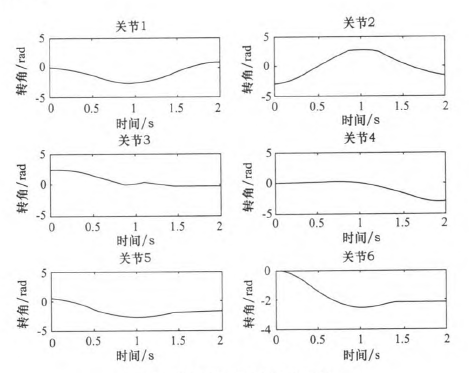
圖9 "353”多項(xiàng)式關(guān)節(jié)角度

根據(jù)仿真結(jié)束所示，該方法可以得到平穩(wěn)、連續(xù)的關(guān)節(jié)角度、角速度和角加速度的變化軌跡。與表3中的三次、五次多項(xiàng)式最大值比較，可以看出相對三次多項(xiàng)式可以得到平穩(wěn)、連續(xù)的角加速度，同時相對五次多項(xiàng)式可以得到比較小的最大關(guān)節(jié)角加速度，從而使整個關(guān)節(jié)運(yùn)動過程中更加平滑，減小了機(jī)構(gòu)間的沖擊。

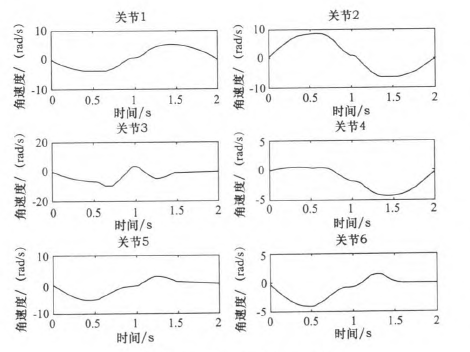
圖10 “353”多項(xiàng)式關(guān)節(jié)角速度

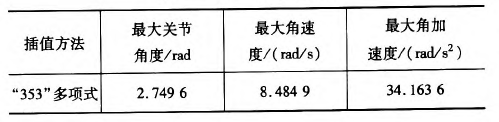
表4“353”多項(xiàng)式最值

3.結(jié)語

本文通過在MATLAB環(huán)境中，基于MZ07工業(yè)機(jī)器人運(yùn)動模型，分析了三次多項(xiàng)式和五次多項(xiàng)式的軌跡插值算法，對比了兩個方法的優(yōu)缺點(diǎn)。關(guān)節(jié)空間在“353”多項(xiàng)式插值規(guī)劃后，通過仿真研究，“353”多項(xiàng)式插值既可以得到平穩(wěn)、連續(xù)的角加速度軌跡，又可以得到較合適的最大角加速度，解決了三次多項(xiàng)式插值后關(guān)節(jié)角加速度不連續(xù)問題和五次多項(xiàng)式插值規(guī)劃后關(guān)節(jié)最大角加速度較大問題。在關(guān)節(jié)空間中多項(xiàng)式插值的高低次結(jié)合使得各關(guān)節(jié)的變換優(yōu)于單一使用的同次多項(xiàng)式插值。

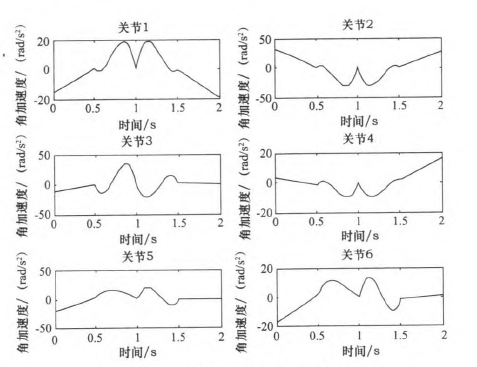
圖11 “353”多項(xiàng)式關(guān)節(jié)角加速度

投稿箱：
如果您有機(jī)床行業(yè)、企業(yè)相關(guān)新聞稿件發(fā)表，或進(jìn)行資訊合作，歡迎聯(lián)系本網(wǎng)編輯部，郵箱：skjcsc@vip.sina.com

更多相關(guān)信息

名企推薦

業(yè)界視點(diǎn)

| 更多

行業(yè)數(shù)據(jù)

| 更多

博文選萃

| 更多

数控机床市场网-专业的数控机床网站

數(shù)控機(jī)床