軸承過盈配合量對主軸動力學特性的影響
2018-2-5 來源: 北京工業大學機械工程與應用電子技術學院 作者:郭鐵能, 馬小超, 谷昀超, 陳劍科
摘 要: 為探索軸承配合過盈量在轉速和溫升等因素影響下的變化規律及對主軸系統動力學特性的影響規律,首先建立了考慮轉速引起的內圈離心膨脹和溫升引起的熱位移軸承過盈配合模型,然后將過盈配合模型耦合進Harries 軸承動力學模型,建立了考慮軸承配合的軸承動力學模型,并基于Timoshenko 理論建立機床主軸系統有限元模型. 針對實驗室自建主軸系統,進行了軸承配合過盈量對主軸動力學特性影響分析. 結果表明:軸承內、外圈初始過盈量增加,原始接觸角線性減小;初始過盈量在溫升及離心力的雙重影響因素下會增大;初始過盈量、內圈離心膨脹及內外圈熱膨脹會導致軸承剛度增大,軸承剛度增大導致主軸系統固有頻率增加,相比較一、二階固有頻率,三、四階固有頻率受過盈量及其影響因素的影響較大.
關鍵詞: 過盈配合量; 有限元; 固有頻率
影響主軸系統動力學特性的因素很多,包括主軸系統受到的驅動力、預緊力和轉速等,然而主軸系統又包括了軸承、主軸等部件,每一個部件及其影響因素對整體主軸系統的動態特性都有影響,許多學者也對主軸系統動力學特性及影響規律做了大量的研究,但涉及主軸軸承配合對主軸系統動力學特性及影響因素的作用規律很少. 2003 年,Lin 等[1] 建立了主軸系統熱-機械力模型,考慮了熱特性、軸承預緊力和剛度的影響,但是其只考慮了軸承的靜態支撐剛度,沒有考慮高速狀態下軸承剛度的變化.2006 年,Chen 等[2] 研究了轉速和載荷對轉子-軸承系統動態性能的影響,發現離心力引起的軸承剛度軟化是引起電主軸系統剛度降低的主要原因,其次是主軸的陀螺效應. 2007 年,British Columbia 大學Cao 等[3] 的主軸系統模型中包含了離心力、陀螺效應,以及軸承接觸角、預載、主軸轉子和軸套偏移等的影響,比較系統地提出了主軸系統的通用建模方法. 湖南大學的張峻暉等[4] 研究高速軸承過盈配合量的計算方法,系統分析了過盈配合的影響因素,但沒有考慮其對軸承及主軸系統動態特性的影響. 中國科技大學的王碩貴[5] 研究了初始過盈配合量和預緊力對軸承剛度的影響,但是沒有考慮由轉速引起的離心力及溫升引起的過盈量的變化. 西安交通大學的田久良等[6] 建立了考慮軸承過盈量的主軸系統熱-力耦合模型,重點分析了離心效應和陀螺力矩對主軸系統動態特性的影響.
本文首先建立了考慮轉速引起的內圈離心膨脹和溫升熱位移等影響因素的軸承過盈配合模型,并將過盈配合模型耦合進Harries 軸承動力學模型,建立了考慮軸承配合的軸承動力學模型. 然后基于Timoshenko 理論建立機床主軸系統有限元模型,并與軸承模型集成,得到整體高速主軸系統的有限元模型. 最后分析了過盈配合量及其影響因素對軸承結構和其動態特性以及主軸系統力學特性的影響規律.
1 、過盈配合量對軸承結構參數影響
角接觸球軸承由滾動體、保持架及內、外圈4 個部分構成,其中為使軸承內外圈嚴格定位,并使配合面不產生間隙,軸承內、外圈分別與主軸和軸承座(或箱體)進行過盈配合,軸承座相對主軸系統是固定的. 初始過盈配合量和預緊力的大小會改變軸承內部的結構參數,軸承內外圈發生徑向變形,接觸角發生改變. 電主軸高速旋轉時,一方面產生的離心力會改變主軸與軸承內圈的過盈配合量,另一方面由于溫度的升高,軸承內、外圈發生膨脹,初始過盈量發生改變,軸承的結構參數將會進一步發生改變,進而影響軸承的動態特性.
1. 1 初始過盈量的影響
根據文獻[7]可知,如果壓力均勻地施加在內圓周或外圓周上,而且壁厚超過直徑的20%,則視之為厚壁圓環. 滾動軸承的套圈壁厚大多為直徑的20%左右,所以將其視為厚壁圓環處理.
軸承內圈與主軸過盈配合,軸承內圈將發生膨脹,軸承內圈溝道直徑將增大,根據彈性力學理論得到內圈溝道的徑向位移[7]
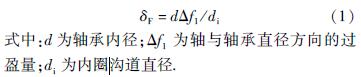
同理,軸承外圈與箱體過盈配合,軸承外圈將收縮,軸承外圈溝道直徑將縮小,外圈溝道的徑向位移為


1. 2 離心力的影響
主軸在高速運轉過程中,由于離心力的存在,軸承內圈會發生徑向變形并對軸承內圈與主軸之間的初始過盈配合量產生影響,而一般軸承外圈與軸承座(或箱體)之間不產生相對運動,所以外圈與軸承座之間的過盈配合不受旋轉導致離心力的影響.承內圈溝道因離心力導致的徑向變形為

式中:Es、μs 分別為主軸的彈性模量和泊松比;dk 為主軸內徑;ρs 為材料密度.
1. 3 溫度的影響
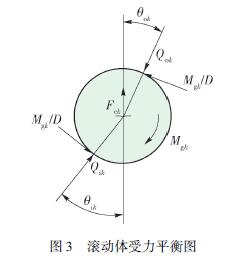
主軸系統高速旋轉過程中,主軸系統內部溫度分布不均勻,圖1 所示為引用文獻[9],預緊力一定的情況下,溫升隨轉速的變化情況. 溫升的變化使軸承內、外圈與主軸外徑均會發生徑向熱變形,而熱變形將會影響軸承與主軸及箱體的過盈配合狀態以及軸承的徑向工作間隙.
考慮主軸影響下的軸承內圈溝道的熱位移為

2 、考慮過盈配合量的軸承動力學建模
圖2 所示為高速軸承載荷作用前后ψk 處軸承內、外圈溝道中心與滾動體中心的幾何關系. 在靜止狀態無載荷情況下,內、外圈溝道曲率中心的距離恒定. 軸承過盈安裝到主軸和箱體并預緊后,軸承接觸角發生改變,內外圈溝道曲率中心距離改變,但是中心依然在一條直線上,當軸承高速旋轉時,由于離心力和陀螺力矩的作用,滾珠中心向外滾道移動,內、外接觸角不再相等. 假設外圈固定,外圈溝道曲率中心不變,內圈溝道曲率中心相對移動.
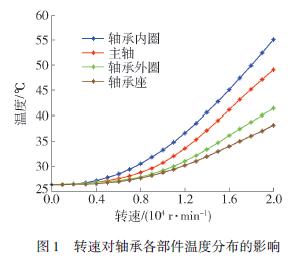
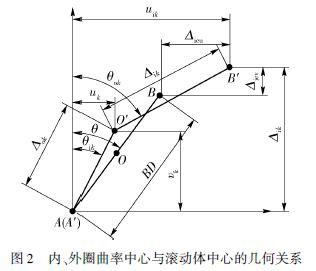
由幾何關系可知,無載荷作用時內、外圈溝道曲率中心之間的距離為




設軸承外圈固定不動,預緊力全部施加在軸承內圈上,將單個滾珠對內圈的作用力求和即可得所有滾珠對內圈的作用力,且與預緊力形成平衡,得到軸承整體受力平衡方程.
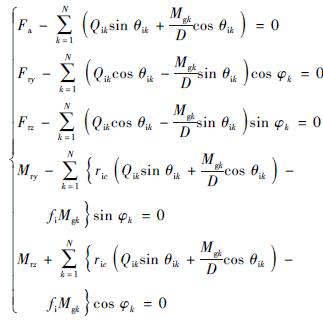
因此,假設軸承包括K 個滾珠,可以聯立這4K +5個方程,建立一個包含4K +5 個方程及4K +5 個未知數的非線性方程組. 求解該方程組即可得到工作狀態下軸承5 個自由度的位移及每個滾珠對應的內外圈接觸力、接觸變形、接觸角等動力學參數.將內圈5 個方向受力對相應位移求導即可得到剛度,即將式(16)中內圈受力對位移求導,將其內部各項分別對位移求導,最終存在4 個未知求導項,即Ukδi 、 Vkδi 、 δikδi 、 δokδi ,引用式(14)和式(15),兩邊對δi 求導,即可得到包含未知項的方程組,迭代求解得到結果,最終能得到剛度.
3 、高速電主軸系統有限元建模
本文基于Timoshenko 梁理論對高速電主軸系統進行有限元建模,模型考慮主軸刀柄和刀具部分,并且刀柄和刀具視為剛性連接,圖4 為主軸系統各部分有限元模型.
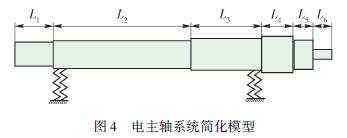
4 、基于過盈量的電主軸系統動態特性分析
本文分析對象為實驗室自建主軸系統實驗臺,采用7212C 角接觸球軸承作為支撐軸承,主軸、刀柄、刀具、軸承具體參數分別如表1 ~ 表4 所示.根據機械設計手冊軸承配合部分,軸承內圈與軸的配合采用基孔制,軸承外圈與軸承座的配合采用基軸制,不同的機構以及不同的負荷狀態選用的配合公差等級不同,不同的公差等級又對應不同的配合量,軸承內外圈的配合狀態也不相同. 一般動圈為過盈配合,靜圈為間隙配合,以機床主軸用7212C 角接觸球軸承為例,內圈為旋轉圈,外圈與箱體固定為靜止圈,假設受載為中等載荷,根據尺寸查表得軸承內圈與軸的過盈配合采


表1 主軸離散單元參數
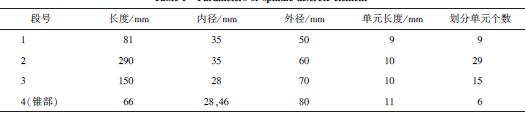
表2 刀柄離散單元參數

表3 刀具離散單元參數

表4 角接觸陶瓷球軸承7212C 參數

4. 1 接觸角的變化
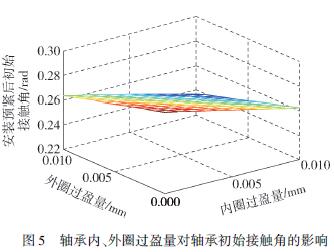
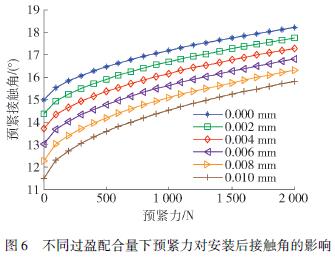
如圖5 所示,軸承過盈安裝后,原始接觸角隨內外圈過盈量的增加線性減小,而施加預緊力后,如圖6 所示,過盈安裝后的接觸角在初始過盈量一定的情況下隨預緊力的增加非線性增加.
4. 2 初始過盈量的變化
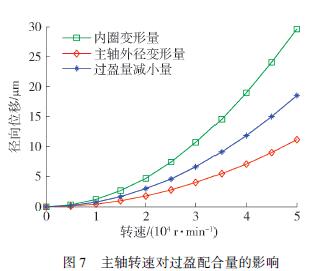
軸承外圈與軸承座(或箱體)之間不產生相對運動,所以外圈與軸承座之間的過盈配合不受旋轉導致離心力的影響. 主要研究旋轉狀態影響下的主軸與軸承內圈的徑向位移的變化,如圖7 所示.從圖7 能看出,隨著轉速的增加,主軸外徑與軸承內圈的徑向位移均呈非線性增長,軸承內圈的變形量始終大于主軸外徑的變形量,因此過盈配合量將減小,并且減小量隨著轉速非線性增加,當轉速在5 000 r/ min 時,過盈配合的減小量為0. 19 μm,基本可以忽略不計,但是當轉速為50 000 r/ min 時,過盈配量的減小量為18. 51 μm,因此在選擇初始過盈配合量時,尤其對于高速主軸系統,必須預先考慮離心力對于過盈配合量的減小效應,提前給予補償,否則軸承可能出現松脫現象.
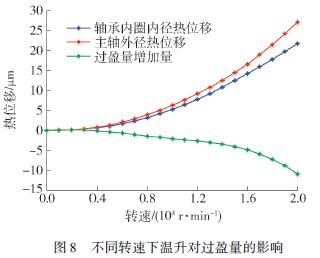
從圖8 能看出,隨著轉速的增加,軸承與主軸的熱位移均增加,當轉速為5 000 r/ min 時,軸承內圈內徑與主軸外徑的熱位移分別為1. 05 μm 和1. 27μm,當轉速為20 000 r/ min 時,熱位移分別為21. 6μm 和27. 1 μm,主軸外徑的熱位移一直大于軸承內圈內徑的熱位移,軸承與主軸之間的過盈量由于溫升熱位移的影響會越來越緊,結合表5 得到,離心力導致的主軸與軸承的徑向位移使過盈量減少,溫升引起的熱位移使過盈量增加,綜合兩方面因素考慮軸承與主軸會越轉越緊.
4. 3 軸承剛度的變化
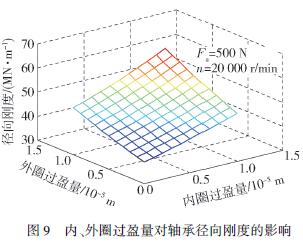
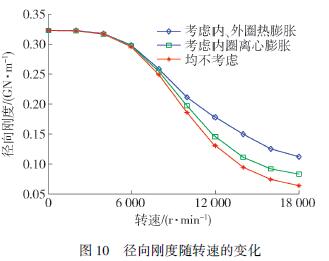
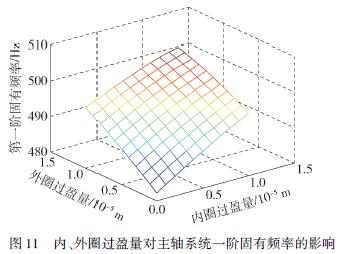
從圖9 能看出,內、外圈初始過盈量增加,軸承徑向剛度非線性增加,主要是因為初始過盈量的增加導致軸承徑向游隙減小,間接提高了軸承的徑向剛度. 由圖10 得知,軸承的徑向剛度隨轉速非線性降低,發生剛度“軟化”現象,其中考慮軸承內、外圈熱膨脹和內圈離心膨脹的徑向剛度較大,隨著轉速的增加差值增大,主要是因為內、外圈熱膨脹和內圈離心膨脹降低了軸承的原始游隙,接觸剛度增大,間接提高軸承的徑向剛度. 4. 4 主軸系統固有頻率的變化在一定的預緊力和轉速情況下過盈量有效提高了軸承的徑向剛度. 以下分析安裝過盈量對高速主軸系統固有頻率的影響,圖11 所示為預緊力為500N、轉速為10 000 r/ min 時,主軸系統一階固有頻率隨軸承內、外圈過盈量的變化規律.
從以上仿真結果能看出,軸承內、外圈過盈量增加,主軸系統第一階固有頻率升高,并且固有頻率隨內、外圈過盈量增長的趨勢與軸承徑向剛度隨過盈量增長的趨勢相近,原因為過盈量有效地提高了軸承的徑向剛度,主軸系統的整體動剛度增加,從而系統固有頻率增加.
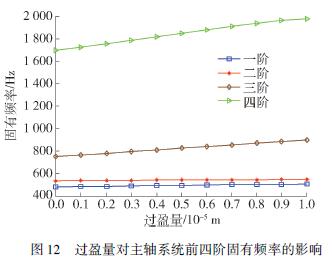
假定軸承內、外圈的過盈配合量相同,同樣設定預緊力為500 N,轉速為10 000 r/ min,具體分析過盈量對前四階固有頻率的影響程度. 圖12 以及表6為過盈量對主軸系統前四階固有頻率的影響.主軸系統在高速旋轉過程中,初始安裝過盈量會受到由于轉速引起的離心力以及溫升的影響,離心力和溫升影響了初始安裝過盈量,進而影響軸承的剛度,主軸系統的動態特性也隨之改變. 以下將分別分析由于軸承內圈離心膨脹和溫升引起熱位移對主軸系統固有頻率的影響,探究預緊力為500 N、初始過盈量為0. 01 mm 時,考慮內圈離心膨脹下固有頻率隨轉速的變化情況. 如圖13 所示.
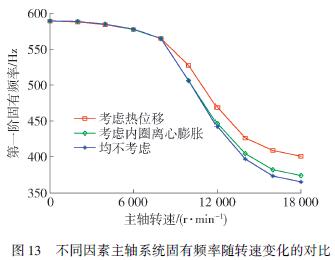
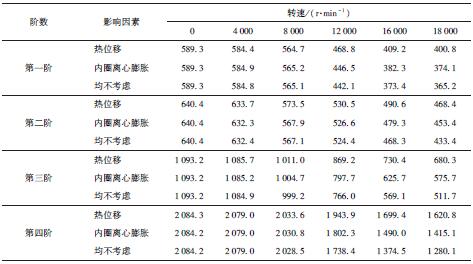
從圖13 能看出,相比較內圈離心膨脹對固有頻率的影響,由于溫升引起的熱位移對主軸系統固有頻率的影響更大,并且隨著轉速的升高,固有頻率的變化增大. 這與前面分析軸承剛度的變化趨勢相同,熱位移與內圈離心膨脹均縮小了軸承的工作間隙,提高了軸承的徑向剛度,并且熱位移的影響大于內圈離心膨脹的影響,最終導致固有頻率的升高.結合表7 所示3 種條件下前四階固有頻率隨轉速變化情況,能看出相比較一、二階固有頻率,三、四階固有頻率受熱位移與內圈離心膨脹的影響較大.
表6 過盈量對主軸系統前四階固有頻率的影響
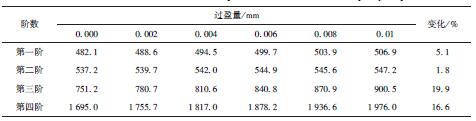
表7 不同因素下前四階固 有 頻率隨轉速的變化
5 、結論
1) 隨著轉速的提高,軸承內部離心力和陀螺力矩的作用顯著,軸承剛度非線性減低,發生“軟化”現象;過盈量提高,軸承剛度明顯增加,而由于轉速引起的離心力和溫升進而導致內、外圈離心膨脹和熱位移對過盈量影響很大,并且導致軸承工作間隙減小,提高了軸承剛度.
2) 隨著轉速的提高,固有頻率呈非線性減小;過盈量增加,主軸系統固有頻率增加,相比較一、二階固有頻率,三、四等高階固有頻率受影響較大.
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com





