螺旋驅動管內機器人自適應運動機理與機構設計
2017-1-20 來源:轉載 作者:-
摘要:為了提高螺旋驅動式管內機器人在直管道和不同曲率半徑彎管道中的環境適應能力,對自適應運動機理這一問題展開研究。考慮管道環境特點,在機器人運動學和力學建模的基礎上,分別提出直行運動機理、轉向運動機理和負載能力調節機理。調節螺旋輪傾角能夠使螺旋驅動式管內機器人具有環境自適應性,并能夠避免運動干涉和滾輪打滑的問題。基于自適應運動機理,提出一種基于自適應聯動機構的螺旋驅動式管內機器人。自適應聯動機構通過偏心臂反饋環境信息,并利用差動原理改變螺旋輪傾角。動力學仿真結果表明:該機器人能夠機械自適應地通過直管和不同曲率半徑的彎管,同時能夠通過自適應聯動機構調節負載能力。
關鍵詞:螺旋驅動;管內機器人;自適應聯動機構;運動機理
0.前言
管道是石油、天然氣、工廠、城市供水系統的主要運輸工具。隨著使用年限的增加,管道容易出現腐蝕、老化、裂縫等故障。近年來,管道事故頻發,造成了巨大的經濟損失和環境破壞。國內外學者開發了各種各樣的管內機器人應用于管道的缺陷檢測和故障維護。相比于傳統的人工檢測方式,機器人檢測具有安全、效率高、成本低等優點。根據移動機構的不同,目前管內機器人主要可以分為9類:pig式[1],內窺鏡式[2],直接驅動輪式[3-4],螺旋驅動式[5-7],履帶式[8],腿式[9],尺蠖式[10],彈力支撐式[11],仿蛇式[12]。
在眾多移動機構中,螺旋驅動方式具有易于微型化和能耗低的優點,在小管徑管道中具有很大應用潛力。國內外的研究學者們對螺旋驅動式管內機器人已經進行了一定研究。IWASHINA等[13]開發的適用于20 mm管徑的螺旋驅動原理的微小型管內機器人;錢晉武等[14]利用螺旋驅動原理開發了管道渦流檢測機器人。以上機器人主要面向直管道環境,在彎管道中的運動能力很差。為了提高機器人的彎管運動能力,HORODINCA等[15]研制了適應40mm、70 mm及170 mm管徑的多款具有萬向軸結構的螺旋驅動管內移動機器人。該機器人雖然能夠通過較大曲率半徑的彎管,但存在運動干涉和滾輪打滑的問題NISHIMURA等[16]開發的基于路徑選擇機構的螺旋驅動式管內機器人雖然具有彎管和T型管道的通過能力,但面對不同曲率半徑的管道需要施加控制,而且由于滾輪不具有單獨調速的能力,依然存在運動干涉和滾輪打滑的問題。以上機器人采用的是螺旋輪傾角固定的結構,機器人的負載能力由電動機性能參數和機器人結構參數所確定。而直彎管內的環境阻力具有較大的變化范圍,固定的負載能力限制了機器人的環境適應性。為了提高機器人對大范圍環境阻力的適應性和電動機的能量利用率,李特等[17]提出了基于螺旋輪傾角可調的管內機器人及相應的能量優化控制策略。
彎管內的運動干涉和打滑問題會加劇機器人傳動部件的磨損,而且不利于機器人的管內定位和能量優化。負載能力可調能增強機器人對大范圍環境阻力的適應性,有利于提高驅動電動機的能量利用率。因此,為了提高螺旋驅動式管內機器人對直管和多曲率半徑彎管的環境適應性,需要首先對機器人的自適應運動機理這一問題進行深入研究,以指導機器人的機構設計。
本文在對螺旋驅動式管內機器人直彎管內建模分析的基礎上,提出了自適應運動機理。自適應運動機理主要包括直行運動機理、轉向運動機理和負載能力調節機理。基于自適應運動機理,提出了一種基于自適應聯動機構的螺旋驅動式管內機器人。通過機構的設計與分析,該機器人能夠滿足自適應運動機理,并具有通過直管和不同曲率半徑彎管的能力。最后通過動力學仿真試驗驗證了機器人運動的有效性。
1.自適應運動機理分析
直彎道和各種曲率半徑的彎管道是工程管道系統的基本結構。由于管道安裝位姿的不同和管內障礙物等,作用于機器人的管內環境阻力具有較大的波動范圍。因此,需要考慮管道的幾何結構和環境阻力因素,對直行運動機理、轉向運動機理和負載能力調節機理展開研究。
1.1 直行運動機理
直管道是最基本的管道類型,將機器人在直管道內的運動機理稱為直行運動機理。忽略重力對運動的影響,機器人的合速度方向始終與管道軸線方向一致。下面建立機器人運動模型,以研究直行運動機理。

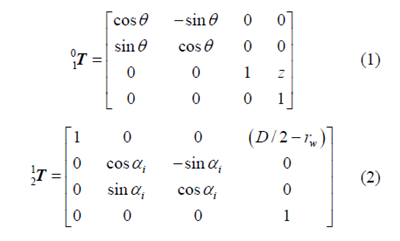
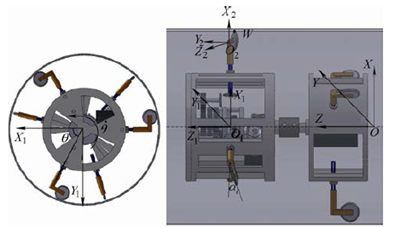
圖1 直管內機器人運動關系示意圖


1.2 轉向運動機理
彎管是管道系統最常用的換向連接部件。彎管中,機器人的轉向運動類似于汽車轉彎的過程。由于各個滾輪在相同時間內的路徑和行程不一致,滾輪速度必須滿足一定的比例關系才能柔順轉向,以避免運動干涉和打滑現象。為了研究彎管轉向運動機理,首先分析機器人轉向時滾輪速度與管道幾何結構參數的關系。
如圖所示 2,在全局坐標系{O}中,彎管幾何約束方程可表示如下
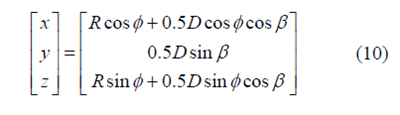
式中,R 表示彎管曲率半徑,φ表示轉向角,β 表示管道徑向截面上的偏轉角。
在圖 2 中,Ri(i=1,2,3)是各滾輪的轉向半徑,vi(i=1,2,3)是各滾輪的速度分量。只有當滿足式(11)時,機器人才能柔順轉向
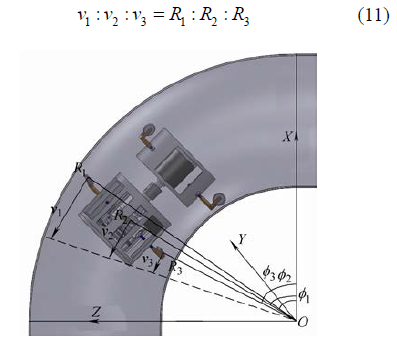
圖2 彎管內機器人轉向運動原理圖

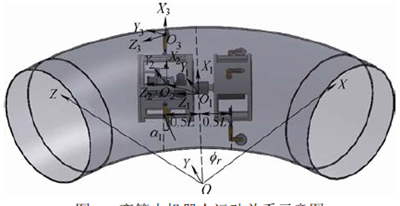
圖3 彎管內機器人運動關系示意圖
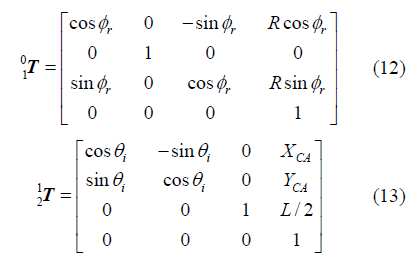


從圖 4 可以看出,彎管轉向運動機理主要有以下關系。
(1) 螺旋輪傾角αi按照一定規律變化可以實現機器人的彎管轉向。
(2) αi的調制規律與彎管曲率半徑有關,曲率半徑越小,αi調整的幅值越大。
(3) αi始終滿足式(18)。當α0是常數,即螺旋輪傾角初值不變時,對等式兩邊進行時間求導, iα.滿足
1.3 負載能力調節機理
管道安裝時位姿各異,受重力、摩擦阻力及纜繩阻力等的影響,管內環境阻力變化范圍較大。因此,為了增強大范圍環境阻力的適應性,需要對負載能力調節機理進行研究。
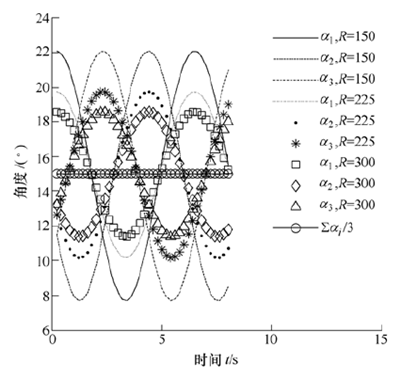
圖4 轉向運動αi自適應調制關系
負載能力是指機器人所能克服的最大環境阻力。當機器人的結構參數、電動機等選定后,負載能力一般是不變的。因此,需要對機器人受力模型進行研究,以分析負載能力調節機理。如圖 5 所示,環境阻力Fa等效地作用在機器人軸線方向,即Xs軸方向。fni和fti分別代表作用滾輪上的法向摩擦力和切向摩擦力。理想情況下滾輪不打滑,因此fni屬于靜摩擦力,fti屬于滾動摩擦力。滾動摩擦力相對很小,在下文分析中忽略不計。螺旋驅動電動機1 輸出轉矩τ,其在滾輪上的等效作用力用Fτ表示。根據Xs軸上的力平衡關系可以得到負載阻力Fa的關系式
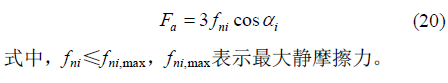
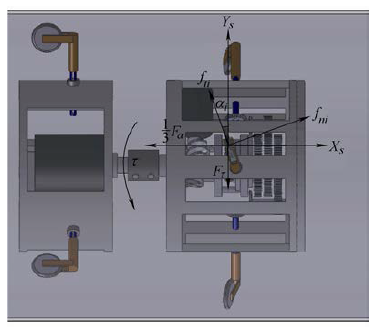
圖5 機器人受力關系示意圖
假設τ足夠大,fni,max由結構參數設定,機器人所能承受的最大環境阻力,即負載能力(記為Fd)僅與αi有關。因此,負載能力調節機理有如下關系。


通過以上分析,自適應運動機理對螺旋驅動式管內機器人的螺旋輪傾角具有以下約束:① 1 個輸入控制3 個螺旋輪傾角輸出;② 3 個角速度之和等于輸入角速度的3 倍;③ 3 個螺旋輪傾角之和等于輸入角度的3 倍;④ 3 個角速度可以成任意比例。這些特性與三軸差速機構的特性相符。0 α. 看作三軸差速機構的輸入,αi看作輸出。通過合理的傳動比設計,可以滿足自適應運動機理的要求。因此,融合自適應運動機理約束,可以得到如圖6 所示的機器人整體設計結構圖。該機器人主要由保持體單元、旋轉體單元兩大部分組成。
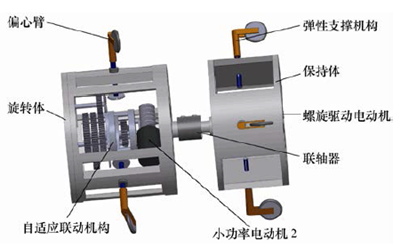
圖6 基于自適應聯動機構的機器人結構圖
保持體單元主要包含保持架、螺旋驅動電動機1、三組120°對稱分布的彈性支撐臂和彈性臂末端的被動滾輪。彈性支撐機構保證末端被動滾輪實時地與管道內壁緊密接觸,而不受管道安裝位姿的影響。電動機1 固定在保持架上,經過減速器后通過聯軸器將動力傳遞給旋轉體的旋轉架。旋轉體在電動機1 的驅動下整體旋轉運動。
旋轉體單元主要包括旋轉架、自適應聯動機構和三組120°對稱分布的彈性支撐臂。彈性臂末端的螺旋輪傾角由自適應聯動機構控制。旋轉體單元旋轉,使被動滾輪對管道內壁產生作用力,該作用反力推動機器人前進。
以上就是融合自適應運動機理約束,提出的一種基于自適應聯動機構的螺旋驅動式管內機器人。
2.2 彈性支撐機構
保持體單元和旋轉體單元各有3 組彈性支撐機構,兩者稍有不同。如圖7a 所示的是安裝在保持體上的彈性支撐機構。它主要由滑桿、套管、滑塊和被動滾輪組成。滑塊在滑槽中的移動能夠改變彈性支撐機構的整體長度。而裝在套管內的壓縮彈簧使彈性臂具有一定的柔性,增加了機器人對臺階、彎管等不規則結構環境的適應性。
如圖 7b 所示,旋轉體單元的彈性支撐機構增加了軸承和傘齒輪。軸承使彈性臂具有一個旋轉自由度。傘齒輪與彈性臂末端固連,并與自適應聯動機構的輸出齒輪相配合。這樣,彈性支撐機構能夠在自適應聯動機構的控制下改變螺旋輪傾角的角度,從而增加了機器人對管道環境的適應性。
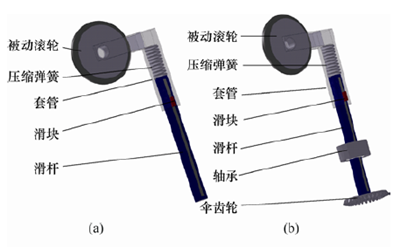
圖7 彈性支撐機構
2.3 自適應聯動機構工作原理
自適應聯動機構利用差動原理和管道環境約束力調節螺旋輪傾角,以滿足螺旋驅動式管內機器人的自適應運動機理需求。
如圖 8 所示,自適應聯動機構以小功率電動機2 作為輸入,三個與螺旋輪傾角固連的傘齒輪作為輸出。電動機2 外殼固定在旋轉架上,并通過蝸輪蝸桿機構將動力傳遞給行星輪系1 的行星架H1。蝸輪蝸桿機構使動力傳遞具有單向性,在電動機2 掉電的情況下也能使行星架H1 保持不動。三個120°對稱放置的行星輪2 通過軸承與行星架H1 相連。太陽輪1 作為輪系的一個輸出端。環齒輪3 與行星輪系2 的行星架H2 同軸且相連。行星輪4 和4′共軸并通過軸承與行星架H2 相連。太陽輪6 和環齒輪5 是輪系的另外兩個輸出。兩組行星輪系組成一個三軸差速機構。行星架H1 是三軸差速輪系的輸入,太陽輪1、太陽輪6 和環齒輪5 是差速輪系的三個輸出。輪系輸出分別通過齒輪傳動機構控制彈性臂上的螺旋輪傾斜角。以太陽輪6 為例:直齒輪6′與直齒輪7 咬合,并通過傘齒輪7′和8 變換旋轉方向,傘齒輪8 與彈性臂桿相連,從而控制螺旋輪傾角。
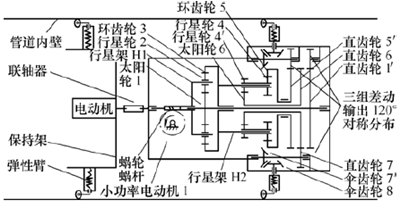
圖8 自適應聯動機構原理圖

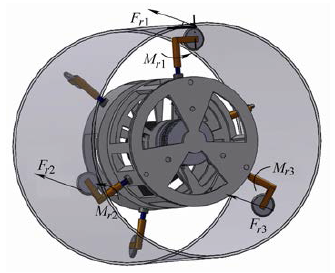
圖9 直管內環境阻力反饋示意圖
從機器人進入彎管開始,由于結構變化,各滾輪受到不同的附加力。在偏心臂機構的反饋下,作用于彈性臂軸向的附加阻力矩也不同,導致阻力矩Mr1≠Mr2≠Mr3,為了使受力重新平衡,避免運動干涉和打滑,自適應聯動機構開始工作。根據最小能耗原理,行星輪2、行星輪4 和行星輪4′開始自轉,調節iα. ,使αi在α0附近變化,從而使滾輪速度滿足式(11)。由于旋轉體是始終旋轉的,各滾輪的移動路徑也在實時改變,因此自適應聯動機構一直工作以滿足轉向速度需求。
2.4 自適應聯動機構的有效性分析
自適應聯動機構輸入與輸出特性與其機構配合關系和齒輪傳動比有關。為了驗證自適應聯動機構的有效性,即能否滿足自適應運動機理的要求,需要對自適應聯動機構的運動關系和受力關系進行分析。
自適應聯動機構的爆炸視圖如圖10 所示。電動機2 是該機構的動力輸入,其與行星架H1 的角速度關系如下


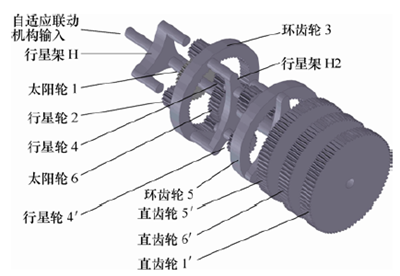
圖10 自適應聯動機構爆炸視圖



3 仿真驗證
為了驗證基于自適應聯動機構的螺旋驅動式管內機器人在直管和各種曲率彎管中運動的有效性,在動力學仿真軟件中做了3 組試驗。分別是直行運動機理、轉向運動機理和負載能力調節機理驗證試驗。表1 中是機器人的設計參數。
表 1 機器人參數

3.1 直行運動機理仿真驗證
機器人在內徑為 150 mm的水平直管道中運動。螺旋輪傾角αi在初始時刻都等于15°。電動機1 以3rad/s的轉速驅動機器人前進。如圖11 所示,αi的值有微小波動,但基本保持在15°附近,而且αi之和始終滿足式(18)。在重力作用下彈性支撐機構不等長,結構非完全對稱,各滾輪移動速度不嚴格相等。因此αi自適應地微調角度,以保持各滾輪具有一致的前進速度。
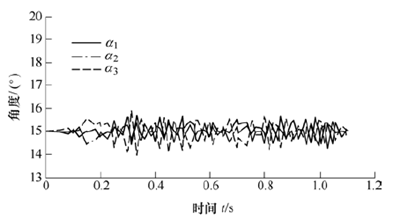
圖11 直管內螺旋輪傾角調制關系
由此可以看出,本文提出的機器人能夠滿足直管內的運動需求。
3.2 轉向運動機理仿真驗證
為了驗證機器人在不同曲率半徑的彎管道中運動的有效性,在仿真中選擇了225 mm和300 mm兩種曲率半徑的彎管。初始角α0都是15°。圖12 顯示了曲率半徑為225 mm時的運動結果。機器人在2s處開始進入彎管,αi在自適應聯動機構的自動調節下開始隨管道結構變化被動改變。在4 s時,機器人完全進入彎管,αi的曲線幅值達到最大±19°,并在4 s到6 s之間變化規律穩定。從第6 s開始,機器人開始駛出彎管,進入直管。αi逐漸回歸到15°附近,以適應直管的管道結構。結果表明:基于自適應聯動機構的機器人能夠機械自適應地通過彎管道環境。
為進一步驗證機器人對不同曲率半徑彎管的適應能力,圖13 給出了曲率半徑為300 mm時的仿真結果。可以看出,αi的曲線與圖中曲線變化規律基本一致。唯一不同的是αi的曲線幅值在最大處只有將近±17°。這是因為曲率半徑增大,彎管結構變化相對較小,因此機器人各滾輪的速度分量vi相差較小,導致αi的調節幅度也比較小。
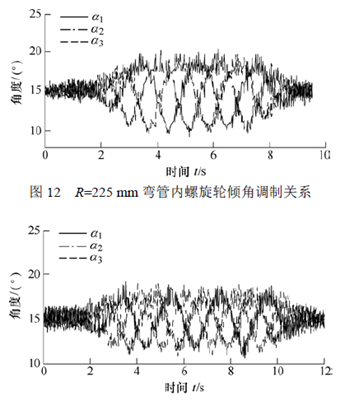
圖13 R=300 mm 彎管內螺旋輪傾角調制關系
因此兩個仿真結果表明機器人可以自適應地通過不同曲率半徑的彎管。
3.3 負載能力調節機理仿真驗證
如圖 14 所示,機器人在一個豎直放置的直管道中運動,并在機器人軸向上作用一個20 N的阻力。如圖14a所示,首先讓機器人以α0等于40°開始運動,可以發現機器人在阻力作用下無法前進。這說明機器人在α0等于40°的情況下無法提供足夠大的負載能力以克服包含重力和摩擦阻力在內的環境阻力。圖14b所示,通過控制電動機2 減小α0,可以發現當α0等于30°的時候機器人能夠前進,但運動不夠穩定,依然伴隨打滑現象。如圖14c所示,當α0等于15°時,機器人能夠穩定的前進。仿真結果說明:通過改變α0的大小,能夠有效地改變機器人的最大負載能力。
4.結論
(1) 本文提出了螺旋驅動式管內機器人在直管、多種曲率半徑彎管和大范圍環境阻力管道內的自適應運動機理,主要包括直行運動機理、轉向運動機理和負載能力調節機理。基于自適應運動機理,本文提出了一種基于自適應聯動機構的螺旋驅動式管內機器人。該機器人通過自適應聯動機構能夠以主動控制和被動自適應兩種方式改變螺旋輪傾角,從而適應管道環境。
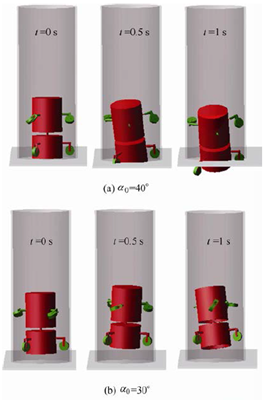
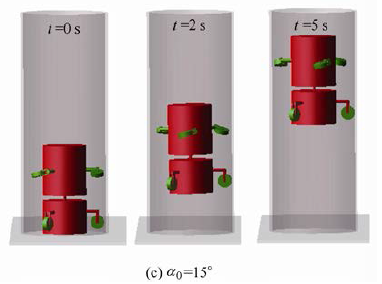
圖14 機器人在相同負載外力以不同α0運動示意圖
(2) 動力學仿真結果表明:基于自適應聯動機構的機器人能夠順利通過直管道和不同曲率半徑的彎管道;通過自適應聯動機構的輸入電動機調整螺旋輪傾角能夠有效改變機器人的負載能力。wen 5
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
更多相關信息





