一種基于位姿反饋的工業機器人定位補償方法
2017-3-6 來源：溫州職業技術學院 溫州大學甌江學院 作者：何慶稀 游震洲 孔向東
0 引言
工業機器人具有高度柔性、通用性和易操作的特性,廣泛應用于汽車、船舶、航空等工業生產領域,特別是因其具有較高的重復定位精度而廣泛應用于焊接、噴涂、搬運等工作中.相對于其較高的重復定位精度,機器人絕對定位精度較低.在工業應用中,影響機器人絕對定位精度的因素很多,主要可以分為兩大因素:一是機器人運動學模型誤差,包括連桿長度誤差、連桿距離誤差;二是機器人動力學模型誤差,主要包括機器人關節傳遞誤差、齒輪傳動誤差、運動摩擦等.目前提高機器人絕對定位精度的方法主要有兩種,一種是對機器人的運動學模型參數進行重新標定.基于運動學模型的參數標定主要包括運動學模型建模、測 量、參數識別和誤差補 四個部 分。
Veitschegger等在DGH模型的基礎上提出了MDGH模型,揭示了機器人連桿參數的微小變化和機器人末端位姿變化之間的線性關系.國內基于模型的參數標定方法普遍是在建立DGH運動學模型的基礎上
,識別出機器人的幾何參數并進行誤差補償.機器人標定技術不僅需要深入研究復雜的機器人正逆運動學模型和參數識別算法,而且存在兩方面的顯著局限,一是補償后定位誤差為０．２mm,精度幾乎沒有提升空間。二是并非對測量空間內所有點均能實現有效補償.另一種提高機器人定位精度的方法是,在工業機器人末端執行器上添加反饋系統,如光學測量系統，視覺測量系統和力檢測系統。wang等使用激光跟蹤儀實時補償工業機器人末端三軸動力頭的運動誤差,但為了降低系統復雜性與成本,該方法只使用在三自由度的機器人上.Vincze等提出了一種采用激光跟蹤儀與視覺系統實時測量機器人位姿的方法,其中機器人的位置信息由激光跟蹤儀獲取,機器人的姿態由激光跟蹤儀與視覺系統共同獲取.
為了提高機器人的定位精度,本文提出一種基于工業機器人末端位置和姿態閉環反饋的定位補償方法.
１ 基于位姿反饋的精度補償原理
１１ 系統組成與集成
基于末端位姿反饋的機器人精度補償系統主要包括工業機器人和 激光跟蹤測量系統兩個部分.工業機器人作為執行主體,主要是實現對末端執行器或工件的夾持和定位.末端執行器或工件通過法蘭盤固定安裝在工業機器人的末端法蘭上,與工業機器人構成一個整體.機器人通過調整末端的位姿來實現末端執行器或工件的定位.激光跟蹤測量系統用于實時地測量機器人末端執行器或工件的位置和姿態，根據剛體的特性,只需要在末端執行器或工件上布置三個以上不在一條直線上的靶標點,就可以實現對位置和姿態的測量.對此,開發了專用的測量軟件,可以通過比較靶標點的設計理論值和激光跟蹤儀的實際測量值,計算末端執行器或工件的位姿偏差.實際上,激光跟蹤儀與工業機器人之間構成了一個基于末端位姿的閉環反饋系統,激光跟蹤儀作為機器人的外置傳感器,實時監測并返回機器人末端的位姿誤差。
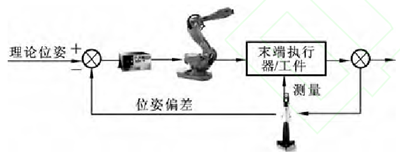
圖1 位姿反饋原理圖
工業機器人和激光跟蹤儀測量系統通過OPC服務器進行數據通信,如圖２所示.這些數據包括位姿偏差數據、機器人坐標系數據等.具體而言,測量軟件驅動激光跟蹤儀完成對靶標點的自動化測量任務,并通過讀取 OPC服務器中的機器人法蘭坐標系數據來計算機器人的位姿偏差,并將偏差數據寫入OPC服務器.機器人在完成定位后需要往OPC服務器中寫入當前機器人法蘭坐標系,并讀取來自測量軟件的位姿偏差數據.
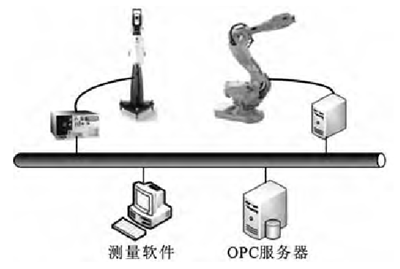
圖２ 系統集成
1.2 位姿補償方法
由于影響機器人本身的定位精度的因素很多,包括運動學模型誤差、齒輪傳動誤差、關節運動摩擦等動力學模型誤差和溫度、載荷等,機器人在位姿補償過程中也會帶入誤差.因此,基于位姿反饋的工業機器人定位精度補償方法的實現是一個逐漸逼近理論位姿的過程,具體操作流程如下:
(１)根據 CAD 模型,確定機器人末端的理論工作位置和姿態,規劃機器人運動路徑,并編制相應的機器人控制程序.根據機器人末端的理論位姿,獲得機器人末端執行器或工件上靶標點的理論坐標.
(２）運行機器人控制程序,實現機器人在自身精度條件下的初定位.
(３)機器人完成定位后,激光跟蹤儀測量靶標點的實際坐標.通過與其理論坐標進行匹配,計算當前機器人末端執行器或工件的位姿偏差.
(４)進行姿態偏差評判,若位姿偏差滿足工藝要求,流程跳轉執行(６);若位姿偏差超出工藝要求,則需要對機器人的位姿進行修正,繼續執行(４).
(５)通過工業局域網絡,激光跟蹤儀將位姿偏差數據傳輸給工業機器人控制系統.工業機器人根據位姿偏差數 據對機器人末端的位姿進行調整.機器人調整完成后,流程返回(３).
(６)機器人定位結束.
２ 機器人末端位姿誤差評價
２.１機器人位姿誤差描述
機器人位姿誤差包括機器人末端在機器人坐標系下的位置偏差和姿態偏差.末端執行器或工件通過法蘭固定安裝在機器人末端后,與機器人法蘭構成一個整體.因此,機器人末端執行器或工件的位姿誤差問題可以轉換為機器人末端法蘭的位姿誤差問題.機器人位姿反饋補償流程如圖３所示.
２.1.1 機器人末端位置誤差
機器人末端的位置誤差表示機器人末端的實際位置和理論位置之間的差值,即：ΔT＝T-To。式中,T 和To分別為機器人末端的實際位置和理論位置.
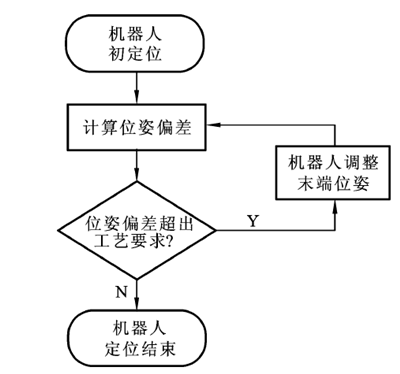
圖３ 位姿反饋補償流程
２.１.２ 機器人末端姿態誤差
機器人末端姿態誤差用四元數表示:Δq＝[q０ q１ q２ q３]＝[cos(θ/２) axsin(θ/２) aysin(θ/２) azsin(θ/２)]式中,[ax ay ax]是對應的歐拉旋轉軸;θ是歐拉旋轉角.
該四元數表示機器人末端的當前姿態和理論姿態的差值,即在當前機器人末端姿態下,機器人末端通過圍繞[ax ay az]T旋轉θ角度后即可得到理論姿態.
姿態四元數和傳統的方向余弦矩陣之間可以通過下面的公式進行轉換: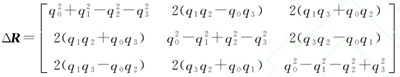
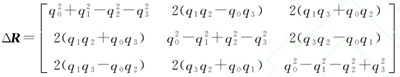
２．２ 位姿誤差評價算法
一個剛體的位置和姿態可以通過不共線的三個點的位置來確定.工件通過法蘭安裝在機器人末端后,可將工件與機器人末端看作是一個剛體.在工件上布置三個以上的靶標點,通過這些靶標點的位置就可以確定當前機器人末端的實際位姿.進一步通過比較靶標點的理論值和實際值,運用剛性匹配算法可以得到機器人末端的位姿偏差.
假設靶標點在機器人坐標系 W 下的理論位置為WPai,實際測量值為WPbi.首先,需要將靶標點的理論值和測量值都轉換到工業機器人的工具坐標系(與機器人末端法蘭坐標系F 重合)下:公式4 5式中,WFT 為機器人末端法蘭坐標系F 到機器人基坐標系W 的齊次矩陣;FTT 為機器人末端執行器或工件坐標系T到機器人末端法蘭坐標系F 的齊次矩陣.
根據剛性匹配原理,靶標點的理論坐標和實際坐標之間滿足如下關系:Pbi＝ΔRPai＋ΔT＋ξi式中,ΔR 和ΔT 分別為姿態偏差和位置偏差;ξi 為第i個靶標點的測量誤差.
為了求解位姿偏差,構建如下最小二乘模型:Σ ＝∑Ni＝||Pbi－ (ΔRPai＋ΔT)||2
式中,N 為靶標點的數量.
令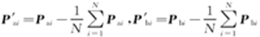
則最小二乘模型可以表示為：
則最小二乘模型可以表示為：
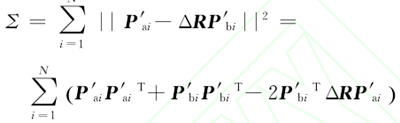
顯然,式(８)的最小化問題等同于求取下式的最大值：
式中,Δq 是姿態誤差 ΔR 對應的四元數.式(９)可以改寫成以下矩陣形式:
此時,姿態誤差四元數 Δq 取矩陣M 的最大特征值對應的特征向量.
最后,位置誤差矩陣可以通過下式計算得到:ΔT ＝P′bi－ΔRP′ai
３ 實驗
本文通過實驗對基于位姿閉環反饋的機器人定位精度和重復定位精度進行了驗證.實驗中,工 業 機 器 人 采 用 庫 卡 公 司 的 重 載 機 器 人KR３６０L２８０Ｇ２(最大載荷２８００N),標稱重復定位精度為０．０８mm.測量設備采用徠卡公司的激光跟蹤儀ATＧ９０１LR.該儀器在全量程范圍內(水平方 向３６０°,垂 直 方 向 正 負 ４５°,最 大 測 量 距 離８０m)對單點的測量不確定度為基礎值１５μm與增量值(每米增量值為６μm)之和.在機器人末端安裝三個靶標點作為位姿檢測點.
為了對機器人在經過位姿閉環反饋補償前后的末端位姿精度和重復定位精度進行比較,在整個機器人的作業空間內隨機選擇了若干位姿作為理論參考位姿.整個實驗過程可以按如下步驟進行:首先,通過機器人運動程序驅動機器人自行運動到目標位姿.在機器人定位完成后,通過激光跟蹤儀測量末端靶標點的坐標,來計算當前的位姿偏差.接著,運用本文提出的基于位姿閉環反饋的位姿精度補償方 法對機器人的末端進行補償,然后記錄補償以后的機器人位姿誤差.最后對補償前后機器人的定位精度進行比較.以其中某個參考位姿的補償過程為例進行說明,圖４記錄了整個位姿補償過程中機器人末端位姿偏差的縮減情況.從圖４可以看出,在經過僅僅三次位姿誤差補償后,機器人的末端位姿便得到了明顯的 提 高,其中 位 置 誤 差 從 １．４ mm 減 少 到０．０８１mm,角度誤差從０．７１２°減少到０．０１３°.顯然,基于位姿閉環反饋的機器人末端位姿補償方法具有很好的收斂性和較高的位姿補償效率.
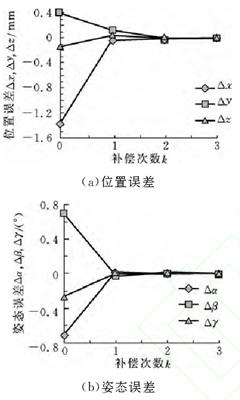
圖４ 機器人位姿補償過程
實驗中,為了獲得經過位姿閉環反饋補償后的機器人的定位精度和重復定位精度,對于每一個參考位姿,重復多次從同一個方向對機器人的位姿進行補償和定位,記錄每次機器人最終實際定位位姿與參考位姿的偏差值.然后計算位姿偏差的均值作為位姿閉環反饋系統的定位精度,同時計算位姿偏差的標準差作為位姿閉環反饋系統的重復定位精度.最后,對工業機器人在位姿反饋補償前后位姿定位精度和重復定位精度進行比較.圖５是工業機器人補償前后的位姿定位精度對比圖,圖中橫坐標為對應的參考位姿編號.從圖中可以非常明顯地看出,經過位姿閉環反饋補償后,工業機器人的末端位姿精度得到了明顯的提高.總體來說,經過補償后工業機器人的末端位置誤差可降低到０.０９mm以下,最大幅度可降低到０．０５mm,姿態誤差降低０．０１５°以下,最大幅度可降低到０．０１２°.相比于補償前,機器人末端位置 誤 差 最 大 幅 度 降 低９５％,姿 態 誤 差 降 低９２％.圖６是工業機器人補償前后的位姿的重復定位精度對比圖,圖中橫坐標為對應的參考位姿編號.從圖中可以看出,經過位姿補償后,工業機器人的重復定位精度也有了很大的提高,其中位置誤差 從 補 償 之 前 的０．０８~０．１４mm降 低 到 了０．０２~０．０５mm,姿態誤差從補償之前的０．０１５°~０．０３°降低到了０．００３°~０．００５°.顯然,實驗結果證明，本文提出的基于位姿閉環反饋的工業機器人定位補償方法可以同時顯著提高機器人的絕對定位精度和重復定位精度.
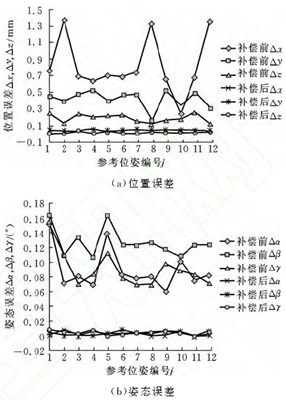
圖5 機器人位姿定位精度比較
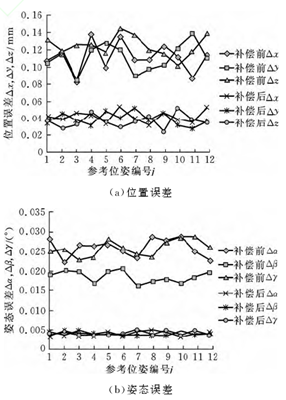
圖6 機器人位姿重復定位精度比較
４ 結論
本文提出了一種基于末端位置和姿態閉環反饋的工業機器人絕對定位補償方法.該方法使用激光跟蹤系統來測量機器人末端上的靶標點來獲得機器人的當前位姿,并通過與靶標點的理論位置匹配來計算機器人末端位姿偏差.工業機器人則根據位姿偏差數據對末端的位姿進行修正.激光跟蹤測量系統與機器人系統通過工業局域網和OPC服務進行數據通信.最后通過實驗驗證了基于位姿閉環反饋的機器人絕對定位補償方法的有效性,實驗結果證明該方法可以顯著降低工業機器人的定位誤差.
投稿箱：
如果您有機床行業、企業相關新聞稿件發表，或進行資訊合作，歡迎聯系本網編輯部， 郵箱：skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表，或進行資訊合作，歡迎聯系本網編輯部， 郵箱：skjcsc@vip.sina.com
更多相關信息
