高速電主軸靜剛度仿真與實驗研究
2018-10-9 來源: 西安理工大學 機械及精密儀器工程學院 作者:崔方圓 李 言 俞嘉藝 湯奧斐 李鵬陽
摘要 主軸靜剛度是評價電主軸靜態特性的一項重要指標,對保證精密數控機床的加工精度至關重要。基于典型工況下切削力和角接觸球軸承徑向剛度計算公式,通過建立的主軸 - 軸承系統三維有限元模型,仿真獲得了在指定工況下電主軸前端軸向變形量及主軸靜剛度。在搭建的實驗平臺上對電主軸進行了靜剛度實驗。通過對比仿真結果和實驗結果,間接驗證了該有限元模型的有效性。基于可靠的有限元模型,進一步仿真獲得了電主軸靜剛度隨前后端軸承預緊力的變化情況。
關鍵詞 靜剛度 電主軸 有限元 預緊力
0、引言
高速電主軸是高檔精密數控機床的核心功能部件,因它在結構上省去了中間傳動環節,由電機直接驅動主軸轉子運轉,所以實現了機床的“零傳動”。主軸靜剛度是評價高速電主軸靜態特性的一項重要指標,它是指主軸受到靜態外載荷作用時抵抗變形的能力,對保證精密數控機床的加工精度至關重要,因此有必要對電主軸系統進行靜剛度研究。
國內外專家學者就電主軸及其靜剛度進行了大量研究。在很早以前,Cao、Altintas 等和 H E JingChang 等就提出了一種較為通用的有限元建模方法,并在靜態下驗證了該模型,使有限元法在電主軸靜態特性分析中有了可靠的 理論依據。Bardac D 和Dogariu C研究了車削加工中心高速電主軸的靜態特性,目的是通過建立的機床主軸系統有限元模型對機床進行設計和優化。國內的孟杰等還專門對高速電主軸的加載實驗進行了研究。王建平等1018-1022研究了陶瓷球軸承接觸角和預緊力對高速磨削電主軸靜剛度的影響,并根據有限元仿真結果,得到了主軸靜剛度關于接觸角和預緊力的擬合方程及擬合曲線。文懷興等利用有限元分析軟件Workbench 對電主軸進行了靜力學分析,目的是驗證電主軸的靜剛度能否滿足工作要求。寸花英等建立了一種加工中心主軸- 軸承系統模型,利用有限元法計算得到主軸系統的靜剛度。
綜合以上文獻可以發現,目前對電主軸靜態性能的研究主要是以建模仿真和有限元分析為主。為了更可靠的檢驗電主軸有限元模型的正確性,需要對其進行加載實驗驗證。針對上述不足,本文分析指定工況下電主軸的受力情況,并將其計算結果應用到有限元模型的計算中。在電主軸靜剛度實驗平臺上進行靜剛度實驗,通過對比仿真結果和實驗結果,驗證了有限元模型的有效性。最后,基于可靠的有限元模型,進一步仿真分析了前后端軸承組不同預緊力對電主軸靜剛度的影響規律。
1、 典型工況條件下主軸受力計算
加工中心在精密加工過程中的大多數加工工藝為銑削加工,因此電主軸所受靜態外載荷主要參考典型銑削條件下的切削力,即作用在銑刀刀齒上的銑削力。根據對刀具和銑削加工運動的影響,作用在銑刀刀齒上的銑削力可分為沿銑刀圓周方向的切削力 Fc、沿銑刀半徑方向的徑向力 Fr及沿銑刀軸線方向的分力 Fa。
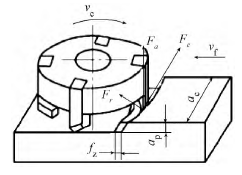
圖 1 為加工中心銑削加工時的受力示意圖。
依據切削力和角接觸球軸承徑向剛度計算公式,可以計算得到作用在電主軸上的軸向分力和軸承組徑向剛度值。
1. 1 確定軸向分力
作用在電主軸上的平均圓周切削力的計算公式為


1. 2 確定軸承組徑向剛度
軸承獲得較好工作狀態的最小預緊力 F 可按下式近似求得

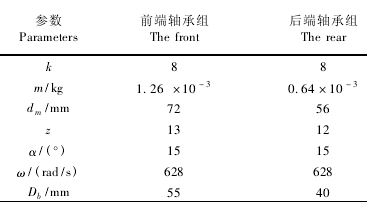
表 1 前后端軸承組參數表
其角接觸球軸承的徑向剛度可按以下剛度計算公式進行計算

2、 電主軸靜剛度的有限元分析
利用有限元分析軟件 LMS Virtual. Lab 對電主軸單元進行靜力學分析。由于該電主軸是階梯軸,具有中空、多支承的結構特點,在建立轉子有限元模型時,需作如下簡化: ( 1) 將角接觸球軸承簡化為彈性支承,忽略其角剛度和軸向剛度,只考慮其徑向剛度;( 2) 忽略軸承負荷對軸承剛度的影響,視軸承剛度為定值; ( 3) 將電機的轉子及過盈套等效為同密度軸材料作為主軸的附加分布質量,等效到所在單元的節點上。簡化后的轉子有限元模型如圖 2 所示。

圖 2 有限元分析主軸模型


圖 3 靜力學求解后的位移云圖
3 、電主軸靜剛度的實驗驗證
本文以實驗室加工中心電主軸為研究對象,其主軸支撐配置方式如圖 4 所示。該型號主軸支撐結構采用一端固定,一端游動的支撐方式,主軸前端為固定端,后端為游動端。電機轉子放在前后軸承組之間.其中前后軸承分別由二聯同向軸承組成,前、后軸承背對背安裝,其中后軸承采用的尺寸較小。
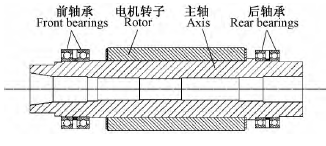
圖 4 主軸支撐配置方式
在進行靜剛度加載實驗時,采用測力環作為加載裝置,對電主軸軸向進行連續加載和卸載,并利用千分表測量主軸前端軸向位移。實驗臺布局如圖 5 所示。

圖 5 實驗臺布局
3. 1 實驗結果分析
圖 6 是由實驗得到的電主軸靜剛度擬合曲線。從圖 6 可以看出,加載曲線和卸載曲線不完全重合,卸載曲線滯后于加載曲線且呈現出明顯的非線性。第一次卸載后,其起點位置也不能恢復到初始位置,但經過多次加載后可以減少殘余變形,最終使加載曲線起點和卸載曲線終點重合。
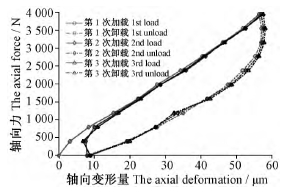
圖 6 軸向靜剛度擬合曲線
根據靜剛度的定義可知加載擬合曲線的斜率即為電主軸系統的靜剛度值。三次加載擬合曲線得到的靜剛度值見表 2。為了盡可能地減小測量誤差,取三次測量值的平均值為最終的靜剛度實驗值。與仿真計算值相比,兩者絕對誤差為 7. 6% ,間接驗證了所建立有限元模型的有效性。

表 2 靜剛度實驗結果
3. 2 誤差分析
(1) 實驗結果比理論結果偏小,這主要是因為仿真分析忽略了系統阻尼、摩擦等因素的影響,這會導致主軸靜剛度實測值比理論計算值偏小。
(2) 實驗得到的主軸軸向靜剛度,特別是卸載曲線的靜剛度呈現出非線性,這主要是由于主軸內部阻尼、摩擦等因素使卸載剛度表現出遲滯現象所導。
(3) 在實驗過程中,實驗結果不可避免的會受到實驗儀器及環境等因素的影響,導致結果出現一定的誤差。
4 、預緊力對電主軸靜剛度的影響
在軸承預緊范圍內,首先取后軸承最小預緊力為128 N 不變,改變前軸承的預緊力,得到電主軸靜剛度隨前軸承不同預緊力的變化曲線,如圖 7 所示。再取前軸承預緊力為其最小值 499 N 不變,改變后軸承預緊力,擬合得到電主軸靜剛度隨后軸承預緊力的變化曲線,如圖 8 所示。由圖 7 和圖 8 可以看出,電主軸靜剛度隨軸承預緊力呈非線性變化規律。由文獻[6]1018-1022知,軸承剛度隨預緊力增大呈非線性增大,最終導致主軸靜剛度也會隨預緊力的變化呈現出非線性。在一定范圍內可以通過增加軸承預緊力來改善電主軸靜剛度,但靜剛度增加趨勢會隨著預緊力的繼續增加逐漸趨于平緩。主軸靜剛度在前軸承預緊力增加的情況下,最大提升幅度約為 15% 左右,而主軸靜剛度隨后軸承預緊力增加時,最大提升幅度約為 7% 。由此可見,電主軸靜剛度對前軸承預緊力變化較大,而受后軸承預緊力的影響很小。
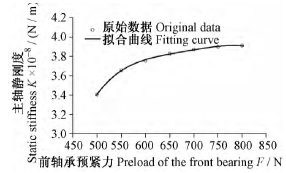
圖 7 主軸靜剛度隨前軸承預緊力的變化曲線
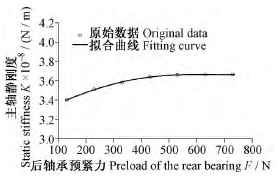
圖 8 主軸靜剛度隨后軸承預緊力的變化曲線
5 、結論
本文利用有限元和實驗相結合的方法,對指定工況下電主軸的受力情況進行了靜力學仿真分析和有限元模型的實驗驗證。重點分析了前后端軸承不同預緊力對電主軸靜剛度的影響。得出以下幾點結論:1) 將電主軸在典型工況條件下的軸向力及軸承剛度計算結果應用到所建立的有限元模型計算中。在利用 LMS Virtual. lab 對電主軸進行靜力學分析時,將軸承支撐用彈性約束來模擬,支撐剛度用軸承剛度來表示,通過有限元法獲得了主軸前端的最大變形量,進而計算得到了電主軸的靜剛度。2) 對仿真結果的有效性進行了實驗驗證。對實測值和理論計算值進行了誤差計算和誤差分析,誤差在可接受范圍內,間接驗證了所建立有限元模型的有效性。3) 通過仿真分析,得出電主軸靜剛度隨預緊力呈非線性增加,且前端軸承預緊力的變化對電主軸靜剛度的影響較大。
投稿箱:
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com
如果您有機床行業、企業相關新聞稿件發表,或進行資訊合作,歡迎聯系本網編輯部, 郵箱:skjcsc@vip.sina.com





